Показатель преломления
Система Максвелла связывает между собой векторы электромагнитной волны группой дифференциальных уравнений. Дифференциальные уравнения, которым должен удовлетворять каждый из векторов поля отдельно, можно получить исключением остальных векторов. Для области поля, которая не содержит свободных зарядов и токов ($\overrightarrow{j}=0,\ \rho =0$) уравнения для векторов $\overrightarrow{B}$ и $\overrightarrow{E}$ имеют вид:
Уравнения (1) и (2) - это обычные уравнения волнового движения, которые обозначают, что световые волны распространяются в среде со скоростью ($v$) равной:
Надо заметить, что понятие скорости электромагнитной волны имеет определенный смысл лишь в связи с волнами простого вида, например плоскими. Скорость $v$ не является скоростью распространения волны в случае произвольного решения уравнений (1) и (2), так как эти уравнения допускают решения в виде стоячих волн.
В любой волновой теории света элементарным процессом считают гармоническую волну в пространстве и времени. Если частота этой волны лежит в интервале $4\cdot {10}^{-14}\frac{1}{c}\le \nu \le 7,5\cdot {10}^{-14}\frac{1}{c}$, такая волна вызывает у человека физиологическое ощущение определенного цвета.
Для прозрачных веществ диэлектрическая проницаемость $\varepsilon $ обычно больше единицы, магнитная проницаемость среды $\mu $ почти равна единице, получается, в соответствии с уравнением (3) скорость $v$ меньше скорости света в вакууме. Что было впервые экспериментально показано для случая распространения света в воде учеными Фуко и Физо.
Обычно определяют не саму величину скорости ($v$), а отношение $\frac{v}{c}$, для чего пользуются законом преломления. В соответствии с данным законом при падении плоской электромагнитной волны на плоскую границу, которая разделяет две однородные среды, отношение синуса угла ${\theta }_1$ падения к синусу угла преломления ${\theta }_2$ (рис.1) постоянно и равно отношению скоростей распространения волн в двух средах ($v_1\ и{\ v}_2$):
Значение постоянного отношения выражения (4) обычно обозначают как $n_{12}$. Говорят, что $n_{12}$ -- относительный показатель преломления второго вещества по отношению к первому, который испытывает волновой фронт (волна) при прохождении из первой среды во вторую.
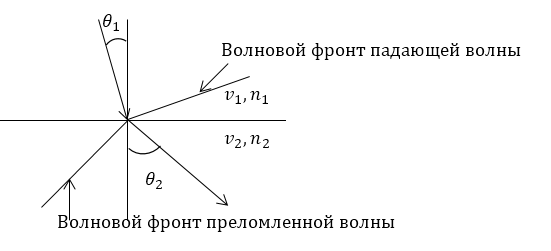
Рисунок 1.
Абсолютным показателем преломления (просто показателем преломления) среды $n$ называют показатель преломления вещества по отношению к вакууму:
\[n=\frac{c}{v}\left(5\right).\]Вещество, имеющее больший показатель преломления является оптически более плотным. Относительный показатель преломления двух веществ ($n_{12}$) связан с их абсолютными показателями ($n_1,n_2$) как:
Формула Максвелла
Максвелл получил, что показатель преломления среды зависит от ее диэлектрических и магнитных свойств. Если в формулу(5) подставить выражение для скорости распространения света из уравнения (3), то мы получим:
\[n=\frac{c}{\frac{c}{\sqrt{\varepsilon \mu }}}=\sqrt{\varepsilon \mu }.\] \[n=\sqrt{\varepsilon \mu }(7).\]Выражение (7) называется формулой Максвелла. Для большинства немагнитных прозрачных веществ, которые рассматриваются в оптике магнитная проницаемость вещества приблизительно можно считать равной единице, поэтому часто равенство (7) применяют в виде:
\[n\approx \sqrt{\varepsilon }(8).\]Часто предполагается, что $\varepsilon $ является постоянной величиной. Однако нам хорошо известны опыты Ньютона с призмой по разложению света, в результате этих экспериментов становится очевидным, что показатель преломления зависит от частоты света. Следовательно, если считать, что формула Максвелла справедлива, то следует признать, что диэлектрическая проницаемость вещества зависит от частоты поля. Связь $\varepsilon $ с частотой поля можно объяснить только в том случае, если принять во внимание атомное строение вещества.
Однако надо сказать, что формула Максвелла с постоянной диэлектрической проницаемостью вещества, в некоторых случаях может быть использована как хорошее приближение. Примером могут служить газы с простой химической структурой, в которых нет существенной дисперсии света, что означает, слабую зависимость оптических свойств от цвета. Формула (8), также хорошо работает для жидких углеводородов. С другой стороны, у большинства твердых тел, например у стекол, и большой части жидкостей наблюдается сильное отклонение от формулы (8), если считать $\varepsilon $ постоянной.
Задание: Какова концентрация свободных электронов в ионосфере, если известно, что для радиоволн с частотой $\nu$ показатель ее преломления равен $n$.
Решение:
За основу решения задачи возьмем формулу Максвелла:
\[n=\sqrt{\varepsilon \mu }\approx \sqrt{\varepsilon }(1.1).\]Для ионосферы можно считать, что $\mu =1.$ Диэлектрическая проницаемость вещества по определению равна:
\[\varepsilon =1+\varkappa =1+\frac{P}{{\varepsilon }_0E}\left(1.2\right),\]где $\varkappa $ -- диэлектрическая восприимчивость, P - мгновенное значение поляризованности. Из (1.1) и (1.2) следует, что:
\[n^2=1+\frac{P}{{\varepsilon }_0E}\left(1.3\right).\]В том случае, если концентрация атомов в ионосфере равна $n_0,$ то мгновенное значение поляризованности равно:
\[P=n_0q_ex_{max}\left(1.4\right).\]Из выражений (1.3) и (1.4) имеем:
\[n^2=1+\frac{n_0q_ex_{max}}{{\varepsilon }_0E}\to n_0=\frac{{\varepsilon }_0E}{q_ex_{max}}\left(n^2-1\right)\left(1.5\right).\]Будем считать, что поле радиоволны изменяется по гармоническому закону:
\[E=E_0cos\omega t\ \left(1.6\right),\]где $\omega $ -- циклическая частота. Уравнение вынужденных колебаний электрона без учета силы сопротивления можно записать как:
\[\ddot{x}+{{\omega }_0}^2x=\frac{q_eE_0}{m_e}cos\omega t\left(1.7\right),\]где $m_e$ -- масса электрона, $q_e$ -- заряд электрона. Решением уравнения (1.7) служит выражение:
\[x=\frac{q_eE_0}{m_e\left({{\omega }_0}^2-{\omega }^2\right)}cos\omega t\left(1.8\right).\] \[x=x_{max}\ при \omega_0=0\to x_{max}=-\frac{q_eE_0}{m_e{\omega }^2}\left(1.9\right)\]Нам известна частота радиоволн, следовательно, можно найти циклическую частоту:
\[\omega =2\pi \nu \left(1.10\right).\]Подставим в (1.5) правую часть выражения (1.9) вместо $x_{max}$ и используем (1.10), получим:
\[n_0=\frac{{\varepsilon }_0E}{q_e(-\frac{q_eE_0}{m_e{\omega }^2})}\left(n^2-1\right)=\frac{{\varepsilon }_0m_e{\omega }^2}{{q_e}^2}\left(1-n^2\right)=\frac{{\varepsilon }_0m_e4{\pi }^2{\nu }^2}{{q_e}^2}\left(1-n^2\right).\]Ответ: $n_0=\frac{E_0m_e4\pi ^2\nu ^2}{{q_e}^2}\left(1-n^2\right).$
Задание: Объясните, почему формула Максвелла противоречит некоторым экспериментальным данным.
Решение:
Из классической электромагнитной теории Максвелла следует, что показатель преломления среды можно выразить как:
\[n=\sqrt{\mu \varepsilon }\left(2.1\right),\]где в оптической области спектра для большинства веществ можно считать, что $\mu \approx 1$. Получается, что показатель преломления для вещества должен быть постоянной величиной, так как $\varepsilon $ -- диэлектрическая проницаемость среды постоянна. Тогда как эксперимент показывает, что показатель преломления зависит от частоты. Трудности, которые возникли перед теорией Максвелла в данном вопросе, устраняет электронная теория Лоренца. Лоренц рассматривал дисперсию света как результат взаимодействия электромагнитных волн с заряженными частицами, которые входят в состав вещества и совершают вынужденные колебания в переменном электромагнитном поле волны света. Используя свою гипотезу, Лоренц получил формулу, связывающую показатель преломления с частотой электромагнитной волны (см. пример 1).
Ответ: Проблема теории Максвелла в том, что она является макроскопической и не рассматривает структуру вещества.












