Соотношение фаз в падающей и преломленной (отраженной) волнах
Используя формулы Френеля:
можно найти фазовые соотношения между отраженной (преломленной) и падающей волнами. Углы падения и преломления всегда находятся в пределах от $0$ до $900$. Следовательно, при любых значениях $\alpha \ и\ {\alpha }_{pr}$, как следует из (1) $E_{pr//}\ и\ $ $E_{pr\bot }$ совпадают по знаку с соответствующими им составляющими ${E_{pad//},E}_{pad\bot }$. Это означает, что на границе раздела веществ фаза волны преломления совпадает с фазой падающей волны.
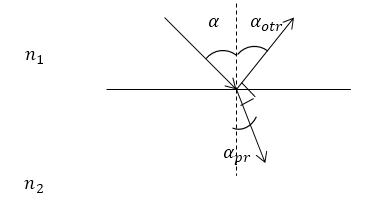
Рисунок 1.
Рассмотрим отраженную волну. Ее составляющая ($E_{otr//}$) совпадает по знаку в соответствующем выражении системы (1) в том случае, если: ${tg \left(\alpha -{\alpha }_{pr}\right)\ } >0\ и\ tg(\alpha +{\alpha }_{pr}) >0$ или ${tg \left(\alpha -{\alpha }_{pr}\right)\ }
при $\alpha >{\alpha }_{pr}$ ($n_{21} >1$) и $\alpha +{\alpha }_{pr}
-
при $\alpha \frac{\pi }{2}$.
Данное отражение составляющей $E_{pad//}$ сопровождается сдвигом по фазе на $\pi $. Отражение параллельной составляющей без сдвига фаз происходит в случаях:
-
при $\alpha >{\alpha }_{pr}$ ($n_{21} >1$) и $\alpha +{\alpha }_{pr} >\frac{\pi }{2}$;
при $\alpha
Для отраженной составляющей волны $E_{otr\bot }$ и $E_{pad\bot }$ совпадают по знаку, и отражение идет без сдвига фаз, в том случае, если $\alpha
Явление Брюстера
Угол падения, при котором сумма углов падения и преломления равна $\frac{\pi }{2}$, называют углом Брюстера (${\alpha }_b$). Используя закон преломления для угла Брюстера:
Если угол падения равен углу Брюстера, то между направлениями отраженной и преломленной плоских волн равен $\frac{\pi }{2}$. Следовательно, ${\alpha }_{pr}+\alpha \frac{\pi}{2}$ при $\alpha >{\alpha }_b$.
Отражение света при $\alpha 1$) ведет к изменению фаз на $\pi \ $(то есть происходит потеря половины волны).
Если свет на границу раздела двух сред падает под углом Брюстера ($\alpha ={\alpha }_b,$ то $tg\left({\alpha }_b+{\alpha }_{pr}\right)=\infty $) в соответствии с системой (1) $E_{otr//}=0$. Это означает, что в отраженном свете колебания вектора напряженности электрического поля происходят только в плоскости, которая перпендикулярна плоскости падения. То есть отраженный свет является полностью линейно поляризованным. Такой результат отражает смысл закона Брюстера.
Надо отметить, что при $n_{12}
Отражение под углом Брюстера - один из способов получения линейно поляризованного света.
Явление Брюстера вызвано поперечностью электромагнитной волны. Под влиянием падающей волны электроны вещества совершают колебания и излучают вторичные волны, которые накладываются на первоначальные колебания. На длине смещения происходит полная замена падающей волны волной, которую излучают электроны при своих колебаниях. Линия колебаний электронов коллинеарна вектору $\overrightarrow{E}$ волны. При равенстве угла падения углу Брюстера, когда угол между преломленной и отраженной волнами составляет $90^\circ$, электроны среды, порождающие преломленную волну, совершают колебания вдоль линии, которая параллельна направлению, в котором должна распространяться отраженная волна. Вдоль линии своих колебаний электрон не может излучать электромагнитную волну. В результате отраженная волна отсутствует.
Исследование процесса отражения света под углами близкими к углу Брюстера дает возможность экспериментально проверить формулы Френеля. Так как интенсивность отраженной под углом Брюстера волны, в которой вектор колеблется в плоскости падения, равна нулю. Данное утверждение удобно для эмпирической проверки, так как при этом не требуется точного соблюдения угла падения. Можно просто непрерывно изменять угол падения около угла Брюстера. При прохождении угла Брюстера интенсивность волны с соответствующей поляризацией обращается в ноль.
Задание: Какова скорость света в кристалле каменной соли, если угол Брюстера при падении пучка света из воздуха составляет ${\alpha }_b=57^\circ$?
Решение:
В качестве основы для решения задачи используем закон Брюстера:
\[{tg(\alpha }_b)=\frac{n_2}{n_1}\left(1.1\right).\]Выразим абсолютный показатель преломления кристалла каменной соли из выражения (1.1), имеем:
\[n_2=n_1{tg(\alpha }_b)\left(1.2\right).\]Показатель преломления света в кристалле связан со скоростью распространения света в нем как:
\[n_2=\frac{c}{v_2}\left(1.3\right),\]где $c$ -- скорость света в вакууме. Приравняем правые части выражений (1.2) и (1.3), получим:
\[n_1{tg(\alpha }_b)=\frac{c}{v_2}\left(1.4\right).\]Выразим из (1.4) искомую скорость ($v_2$), получим:
\[v_2=\frac{с}{n_1{tg(\alpha}_b)}.\]Проведем вычисления, зная, что для воздуха $n_1=1,c=3\cdot {10}^8\frac{м}{с}\ $:
\[v_2=\frac{3\cdot {10}^8}{tg(57{}^\circ )}=1,94\cdot {10}^8(\frac{м}{с}).\]Ответ: $v_2=1,94\cdot {10}^8\frac{м}{с}$.
Задание: Каков двугранный угол стеклянной призмы $\theta ,$ на который падает пучок естественный света, если отраженный свет максимально поляризован. Показатель преломления вещества призмы равен $n$.
Решение:
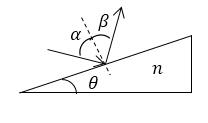
Рисунок 2.
В качестве основы для решения задачи используем закон Брюстера:
\[{tg(\alpha }_b)=\frac{n_2}{n_1}\left(2.1\right).\]Из выражения (2.1) выразим угол падения:
\[{\alpha }_b=arctg\left(\frac{n_2}{n_1}\right)\left(2.2\right).\]Из рис. 2 видно, что искомый угол равен:
\[\theta =\frac{\pi }{2}-{\alpha }_b=\frac{\pi }{2}-arctg\left(\frac{n_2}{n_1}\right).\]Если пучок света первоначально распространяется в воздухе, то $n_1=1,$ по условию $n_2=n.$
Ответ: $\theta =\frac{\pi }{2}-arctg\left(\frac{n_2}{n_1}\right).$











