Интегралы Френеля
Интегралы вида:
\[C\left(s\right)=\int\limits^s_0{cos (\frac{\pi {\xi }^2}{2})d\xi },\ S\left(s\right)=\int\limits^s_0{{sin \left(\frac{\pi {\xi }^2}{2}\right)\ }d\xi }\left(1\right).\]называют интегралами Френеля. Их вычисляют, используя численные методы (существуют таблицы данных интегралов). При $C\left(\infty \right)=S\left(\infty \right)=0,5;\ C\left(-\infty \right)=S\left(-\infty \right)=-0,5.$
Графически данные таблицы представлены в виде спирали Корню (рис.1).
Спираль Корню
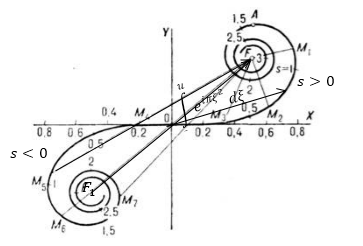
Рисунок 1.
Комплексное число равное:
можно изобразить комплексным вектором, который начинается в начале координат и заканчивающемся в точке на спирале Корню, которая соответствует значению $s$ (рис.1).
Данная спираль состоит из двух симметричных ветвей, которые закручены вокруг фокусов ($F$). Верхняя ветвь представляет действие правой половины фронта, а нижняя ветвь соответствует левой части фронта. Отличие от спирали Френеля вызвано более быстрым убыванием начальных зон Шустера, чем зон Френеля.
Допустим, что на пути распространения плоской волны света размещается непрозрачный плоский экран с прямым краем. В таком случае левая часть спирали Корню описывает результат колебаний, которые приходят в точку наблюдения от участков поверхности волны (если бы они были открыты), тех, что лежат левее края непрозрачной полуплоскости.
Амплитуда колебаний в точке наблюдения ($B_0$) от волновой поверхности, которая расположена правее края преграждающего экрана изображается вектором, проведенным из точки $O$ в фокус $F$. Амплитуда колебаний в точке наблюдения, от полностью открытой волновой поверхности определяется вектором, который соединяет фокус нижний левый и верхний правый.
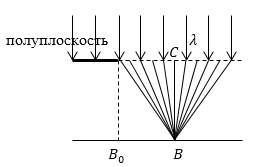
Рисунок 2.
Спираль Корню используют как метод анализа дифракции. Она позволяет анализировать количественно распределение интенсивности в картине дифракции.
Применение спирали Корню для нахождения амплитуды колебаний
Для того чтобы отыскать амплитуду колебаний в точке наблюдения, которая находится правее $B_0$ (рис.2) от какой - то полосы волновой поверхности, следует построить вектор, который замыкает участок спирали Корню, соответствующий исследуемой полосе.
Схема действий такова. Любой точке спирали Корню соответствует некоторое значение параметра $s$ (этот параметр пропорционален длине дуги спирали, которая берет начало в точке $О$ рис.1). Значения параметра указываются на кривой. Данный параметр определен выражением:
где $\lambda $ - длина волны света, $l$ - расстояние между экраном и волновой поверхностью, $x$ - расстояние от точки $C$ (рис.2) до рассматриваемой точки. Так как параметр $s$ пропорционален расстоянию $x$, то это расстояние пропорционально длине дуги спирали Карню (отсчет от точки $O$).
Для дифференциала дуги спирали Корню имеем:
Используя спираль Корню, надо знать значение параметра $s$. Его легко найти, если известно расстояние $x$ точки наблюдения от центра картины. Вычислив ширину первой зоны Шустера ($\sqrt{\lambda l}$), далее найдем $s$ по формуле (3).
Применение спирали Корню для нахождения интенсивности света
Рассмотрим механизм нахождения распределения интенсивности, используя спираль Корню. Найдем ее на экране около края геометрической тени в случае дифракции плоской волны от прямого края непрозрачной полуплоскости (рис.2). В том случае, когда точка $B$ лежит правее $B_0$ (рис.2), то правая часть поверхности волны полностью открыта (от точки $C$). В таком случае на спирали амплитуда колебаний в точке наблюдения соответствует вектору $\overrightarrow{M_5F}$ (рис.1). Начало данного вектора определено положением точки наблюдения. В случае, если это точка $B_0$(край геометрической тени), то точка начала вектора совпадает с точкой $O$ спирали Корню, его вектор -- амплитуда колебаний изображается вектором $OF$, который равен половине вектора $\overrightarrow{F_1F}$ от открытой полностью волновой поверхности. Следовательно, интенсивность света в точке $B_0$ меньше в 4 раза интенсивности при отсутствии преград.
В том случае, если точка наблюдений перемещается в правую сторону от точки $B_0$, то начало вектора на спирали Корню движется по левой ветке спирали (слева от точки $C$ открываются новые зоны). В результате амплитуда и интенсивность в точке $B$ будет меняться от максимума к минимуму. Различие между ними при удалении точки $B$ от $B_0$ будет постепенно девальвироваться. При этом интенсивность света приближается к $I_0\ (интенсивность\ падающего\ света)\ (рис.3).$
Если точка наблюдения перемещается от точки $B_0$ в область геометрической тени, то начало вектора на спирали Корню движется вправо от точки $O$. При этом длина вектора, соответственно интенсивность света монотонно уменьшается до нуля (рис.3).
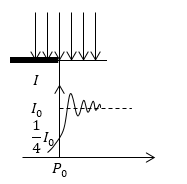
Рисунок 3.
Задание: Найдите расстояние между первыми двумя максимумами на экране, если картина дифракции наблюдается от края непрозрачной полубесконечной плоскости, которая находится на расстоянии $l=1м\ $от экрана. Длина волны света равна $\lambda=0,5\cdot {10}^{-6}$м.
Решение:
Расстояние между максимумами можно найти в соответствии с формулой:
\[\triangle x=x_2-x_1\left(1.1\right).\]Далее используем формулу для параметра $s$ спирали Корню, из которой выразим $x$:
\[s=x\sqrt{\frac{2}{\lambda l}}\to x=s\sqrt{\frac{l\lambda }{2}}\left(1.2\right).\]Соответственно, для $\triangle x$ имеем:
\[\triangle x={(s}_2-s_1)\sqrt{\frac{lл}{2}}(1.3).\]Проведем вычисления:
\[\triangle x=\left(2,3-1,2\right)\sqrt{\frac{1\cdot 0,5\cdot {10}^{-6}}{2}}=5,5\cdot 10^{-4}\left(м\right).\]Ответ: $\triangle x=5,5\cdot 10^{-4}$м.
Задание: Используя понятие касательной к спирали Корню объясните, как ведет себя спираль.
Решение:
Пусть угол наклона касательной к спирали Корню в избранной точке будет равен $\alpha $, тогда можно записать, что:
\[tg\alpha =\frac{dS}{dC}\left(2.1\right).\]Уравнение спирали Корню в параметрическом виде:
\[C\left(s\right)=\int\limits^s_0{cos (\frac{\pi {\xi }^2}{2})d\xi },\ S\left(s\right)=\int\limits^s_0{{sin \left(\frac{\pi {\xi }^2}{2}\right)\ }d\xi \left(2.2\right).}\]Из уравнений (2.1) и (2.2) следует, что:
\[tg\alpha =tg\left(\frac{\pi s^2}{2}\right)\to \alpha =\frac{\pi s^2}{2}\left(2.3\right).\]Если $s=0$, то $\alpha =0$, что означает, кривая Корню в начале координат касается оси $X$. При s=1, $\alpha =\frac{\pi }{2}$, кривая Корню идет вверх. При $s=\sqrt{2}$, $\alpha =\pi $, касательная горизонтальна, но идет против оси $X$. При $s=\sqrt{3}$, $\alpha =\frac{3}{2}\pi $, касательная вертикально идет вниз. При $s=2$, $\alpha =2\pi $, касательная в горизонтальном направлении (исходном). Так выражение (2.3) объясняет, как спираль Корню обвивается вокруг своих фокусов ($F,\ F_1$) рис.1. Совершая бесконечно много оборотов.











