Когерентностью называют пространственную и временную корреляцию отдельных электромагнитных колебаний по частоте и фазе. Частным случаем когерентного излучения является монохроматическая волна, ее частота находится в узком диапазоне частот, фаза такого излучения не является строго фиксированной.
Степень когерентности двух световых пучков ($\gamma $) определяют как:
\[\gamma =\frac{I_{12}}{\sqrt{I_1I_2}}=0\div 1\left(1\right),\]где $I_{12}$ - функция взаимной когерентности двух пучков света с интенсивностями $I_1{и\ I}_2$. В идеально когерентны пучках света, степень когерентности равна $1$. На практике излучение считают когерентным если $\gamma =0,98.$ Степень когерентности и ее временные и пространственные характеристики измеряют при помощи интерферометров.
В интерферометрии до применения лазеров в качестве источников света использовали обычно газоразрядные и твердотельные счетчики света. Очень важным в классической интерферометрии является создание оптического поля с высокой когерентностью и большой мощностью излучения. Подобное сочетание параметров излучения могло бы обеспечить решение большого числа задач оптики в области, например, измерений. Но, следует заметить, что сочетание большой степени когерентности и высокой интенсивности излучения для источников света не лазерного характера имеет ряд противоречий. Так как увеличение степени когерентности связано для подобных источников света с неизбежным уменьшением интенсивности излучения. Этот факт легко объяснить, так как повышение значения любого параметра когерентности для волнового поля имеет связь с его фильтрацией пространственной или частотной, и это ведет за собой потерю интенсивности поля.
Степень когерентности излучения, которое испускается любыми двумя точкам не точечного (имеющего конечные размеры источника света), уменьшается при увеличении расстояния между этими двумя точками. Если рассматривать плоский, квазимонохроматический, однородный источник света $S$, имеющий радиус $R$, который освещает экран $Э$, параллельный источнику света и находящийся на расстоянии $L$ от него, причем $L\gg R\ (рис.1)$, то по теореме Ситтера - Цернике, диаметр круга на экране, в пределах которого излучение можно считать когерентным (почти) равен:
где $\varphi =\frac{R}{L}$ - угловой размер источника света относительно точки, в которой ведется наблюдение.
Так, для того, чтобы от некогерентного источника света получить когерентный пучок света (плоскую монохроматическую волну), обладающий конечным поперечным сечением, следует источник света поместить на большом расстоянии от точки наблюдения. Либо надо иметь точечный источник света, размерами которого можно пренебречь.
При этом следствием выделения когерентного пучка света является то, что используется только небольшая часть энергии излучаемой источником.
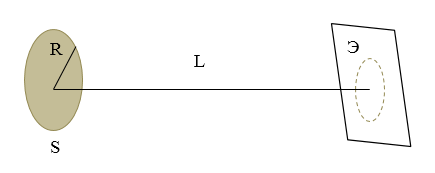
Рисунок 1.
Принципиально иная ситуация складывается в отношении лазерного излучения. Лазеры, с одной стороны имеют высокую мощность излучения, с другой стороны исключительно высокую пространственную и временную когерентность испускаемого волнового поля. В отличие от тепловых источников света лазеры характеризует сильная связь между атомами, которые излучают волны и полями, которые они создают. Причина такой связи заключена в механизме вынужденного испускания света. Кроме того, сказывается то, что нелинейность среды связывает разные виды колебаний в резонаторе лазера.
Пространственные фильтры
Пространственной фильтрацией называют целенаправленное воздействие на структуру потока излучения для того, чтобы придать ему необходимые свойства (например, малую расходимость) или для обработки информации, которая переносится данным потоком.
Пространственной фильтрацией изображения называют внесение изменений в изображение предмета с помощью модификации дифракционной картины предмета, из которого потом будет сформировано изображение.
Изменение изображения путем воздействия на распределение амплитуд (не на само изображение), которые составляют его, является сутью пространственной фильтрации. Основной задачей при этом является конструирование фильтра, который необходимым образом изменяет волну, которая распространяется через него.
Для конструирования таких фильтров в инфракрасной области спектра и области не слишком коротких волн ультрафиолетового излучения применяют фокусирующие элементы (линзы, зеркала). Для электромагнитных волн, имеющих длины порядка рентгеновского излучения с целью выделения узкого пучка параллельных лучей используют последовательность экранов с отверстиями, которые расположены вдоль одной линии.
Основной идеей оптической пространственной фильтрацией является идея использовать использования амплитудных, фазовых, амплитудно-фазовых оптических фильтров (световых фильтров, фазовых пластинок, диафрагм, голограмм и др), которые помещают в месте распределения фурье - спектра, которое передаётся через оптическую систему изображения. Так имеющийся спектр трансформируют необходимым образом.
Эксперимент Аббе - Портера первым показал возможность пространственной фильтрации изображений. В этом эксперименте в качестве предмета использовалась плоская решетка из штрихов, которые пересекаются под прямым углом. Картина дифракции рассматривалась в фокальной плоскости линзы. При этом входным изображением являлась двумерная дифракционная решетка, ее пространственный спектр - двумерный массив ярких точек (кружков Эйри). В ходе эксперимента использовался пространственный фильтр в виде щелевой диафрагмы, который пропускал составляющие спектра, которые расположены только вдоль одной из осей. Как результат фильтрации в выходной плоскости изображения образуется одномерная решетка.
Цернике предложил применять так называемый фазовый контраст в качестве пространственного фильтра. Такой фильтр характеризуют амплитудным пропусканием, которое имеет вид:
где $H$ - функция пропускания, параметры $u,\ \nu $ - пространственные частоты фурье - представления. Этот фильтр выполняют как диэлектрическую пластинку с толщиной кратной нечетному $\frac{\lambda }{4}$. Пластинка устанавливается строго в центре фокальной плоскости микроскопа. Цель всех манипуляций сводится к тому, чтобы ввести искусственный сдвиг фазы равный $\frac{\pi }{2}$ между волнами, которые соответствуют пространственным частотам нулевого и других порядков дифракции. Такой прием используют в микроскопии в биологии.
Пространственный фильтр с комплексным пропусканием:
обеспечивает на выходе распределение поля, которое соответствует частной производной двумерного распределения сигнала на входе.
Пространственный фильтр Вандер Люгта в котором используется тонкая амплитудная голограмма используется для распознавания оптических изображений.
В условиях лаборатории пучок света с длиной волны $\lambda =589мкм$ пропускают через отверстие диаметром $1мм$. Чему будет равен диаметр когерентности пучка ($d_1$) на расстоянии $2м$? Угловой радиус Солнца при наблюдении с Земли равен $\varphi =0,0093\ рад$, средняя длина волны солнечного света равна ${\lambda }_{ср}=500\cdot {10}^{-9}м$, чему равен диаметр когерентного пучка ($d_2$) в этом случае ?
Решение:
Для вычисления диаметра когерентного пучка света при заданных лабораторных условиях используем формулу:
\[d=0,16\frac{\lambda }{R}L\left(1.1\right).\]Вычислим искомый диаметр, используя данные из условий задачи ($\lambda =589мкм=589\cdot 10^{-9}м,\ \ R=\ \frac{{10}^{-3}}{2}м$):
\[d_1=0,16\cdot \frac{589\cdot 10^{-9}\cdot 2}{{10}^{-3}}\cdot 2\approx 0,4\cdot {10}^{-3}\left(м\right).\]Для того чтобы вычислить диаметр когерентного пучка Солнечного света применим формулу:
\[d=0,16\frac{\lambda }{\varphi }\left(2.1\right),\]Проведем вычисления, учитывая, что ${\lambda }_{ср}=5,5\cdot {10}^{-4}мм=5,5\cdot {10}^{-7}м:$
\[d_2=0,16\frac{5,5\cdot {10}^{-6}}{0,01\ }=9\cdot {10}^{-5}\left(м\right).\]Ответ: $d_1=0,4\cdot {10}^{-3}м,$ $d_2=9\cdot {10}^{-5}$м.
Объясните, почему применяют пространственный фильтр Цернике для исследований в микробиологии.
Решение:
Интенсивность выходящей волны в плоскости изобразительной системы микроскопа зависит от фазы предметной волны, которая определена структурой исследуемого прозрачного объекта. Большое число биологических объектов, например клетки, хромосомы, являются прозрачными. Предметную волну можно представить функцией:
\[f=e^{i\varphi (x,y)}\approx 1+i\varphi \left(x,y\right)\left(2.1\right).\]В микроскопе интенсивность изображения на выходе можно представить как:
\[I={\left(1+i\varphi \left(x,y\right)\right)}^2\approx 1\left(2.2\right).\]Получается, что информация о фазе этой волны теряется. Для исследования объектов в микробиологии в микроскопе используют пространственный фильтр Цернике, который характеризуют функцией амплитудного пропускания:
\[H=e^{-p\left(u^2+{\nu }^2\right)}e^{i\frac{\pi }{2}}(2.3)\]При этом функция интенсивности выходящей волны принимает вид:
\[I={\left\{e^{i\frac{\pi }{2}}+i\varphi \left(x,y\right)\right\}}^2\approx 1+2\varphi \left(x,y\right)\left(2.4\right).\]Таким образом, структура объекта, то есть неоднородности в распределении материала, проявляются в виде неоднородного распределения световой мощности изображения, то есть ее можно наблюдать.











