
Анализ двойного лучепреломления проводят с использованием построения, которое было предложено Гюйгенсом. Этот метод -- обобщение построения для изотопных сред (с его помощью получается закон Снеллиуса). Гюйгенс ввел следующий постулат:
Элементарная волна в кристаллах состоит из двух волн сферической и эллипсоидальной. Сферические волны вызывают к жизни обыкновенную волну. Тогда как эллипсоидальные - необыкновенную. Данный постулат Гюйгенса оправдывается только для оптически одноосных кристаллов.
Он проводится с использованием лучевых поверхностей. Построение Гюйгенса для положительного кристалла изобразим на рис.1. Оптическая ось кристалла при этом, направлена под произвольным углом к поверхности кристалла. Отрезок примем за единицу. Точка считается центром сечения лучевой поверхности.
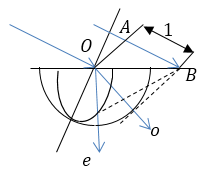
Рисунок 1.
Радиус окружности сечения для обыкновенного луча равен:
Эллиптическое сечение для необыкновенного луча делается так, чтобы расстояние от центра до точки эллипса было равно:
Затем из точки B строят касательные к окружности и эллипсу. Прямые, которые проведены через точку и точки касания -- искомые лучи: обыкновенный -- это тот, который проходит через точку касания к окружности и необыкновенный, проходящий через точку касания на эллипсе. На рис.1 изображена самая простая ситуация, когда падающий луч находится в главной плоскости кристалла, что позволяет сделать все построение Гюйгенса в плоскости чертежа.
В том случае, если входящий луч не принадлежит главной плоскости, то построение Гюйгенса должно быть пространственным. Тогда строят эллипсоиды, сферы и плоскости, однако принцип поиска преломленных лучей не изменяется. Преломленные лучи из центра сечения проходят через точки касания эллипсоида и сферы с соответствующими плоскостями.
Так, явление двойного лучепреломления на границах анизотропных сред Гюйгенс объяснил, используя свои построения, которые основаны на сечениях лучевых поверхностей. Каждая точка фронта, достигая границы раздела, становится источником вторичного возмущения, образуются две волновые поверхности: обыкновенная и необыкновенная. Результирующий фронт является огибающей данных поверхностей, а лучи проходят через точки касания огибающих. Направления волновых векторов в анизотропных средах подчиняются закону Снеллиуса (с разными показателями преломления для обыкновенной и необыкновенной волн). Но, направления лучей не могут определяться с использованием закона Снеллиуса, так необыкновенный луч не обязательно лежит в плоскости падения.
Теорема о связи между лучевой поверхностью и поверхностью нормалей
Даная теорема позволяет провести построения по методу Гюйгенса. Она формулируется следующим образом: Касательная плоскость к лучевой поверхности перпендикулярна к соответствующей волновой нормали и отсекает на ней отрезок, который равен нормальной скорости волны. Из чего следует, что лучевая поверхность -- огибающая плоских волн, которые распространяются из ее центра за единицу времени в разных направлениях. Данными положениями установлена геометрическая связь между лучевой поверхностью и поверхностью нормалей. Следует добавить, что касательная плоскость к лучевой поверхности - фронт волны, который соответствует лучу, проводимого в точку касания.
В данном виде теорема имеет простую интерпретацию. Лучевая поверхность - поверхность равных фаз, до которой возмущение доходит от точечного источника за с. Бесконечно маленький участок такой поверхности можно рассматривать как плоский. Если размеры подобного участка велики, то его распространение будет довольно точно подчинено законам геометрической оптики. В соответствии с такими законами, участок распространяется как бесконечная плоская волна в направлении луча. Значит, волновой фронт -- касательная плоскость к лучевой поверхности. Данная простая интерпретация не заменяет строгое доказательство.
Теорема о связи между лучевой поверхностью и поверхностью нормалей дает возможность построить одну поверхность, если известна другая.
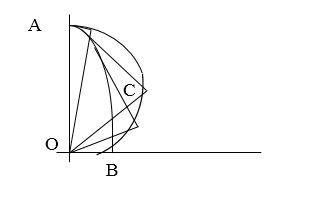
Рисунок 2.
Пусть, участок является участком лучевой поверхности с центром . Проведем в каждой точке заданной поверхности касательную плоскость и опустим на нее перпендикуляр из центра . При этом геометрическое место оснований данных перпендикуляров -- поверхность нормалей.
Чтобы по известной поверхности нормалей построить лучевую поверхность, следует из центра построить во всех направлениях радиус- векторы, потом в точках пересечения их с поверхностью нормалей строят плоскости, которые перпендикулярны данным векторам. Лучевая поверхность - огибающая построенных плоскостей.
Проведите построения Гюйгенса обыкновенного и необыкновенного лучей, если свет падает на одноосный кристалл, если главной плоскостью является плоскость рисунка, оптическая ось () перпендикулярна поверхности положительного кристалла.
Решение:
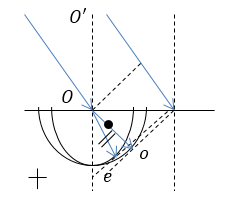
Рисунок 3.
направления колебаний электрического вектора указаны точками (перпендикулярно плоскости рис.) и параллельными отрезками ( в плоскости рис.).
Проведите построения Гюйгенса обыкновенного и необыкновенного лучей, если свет падает на одноосный кристалл, если главной плоскостью является плоскость рисунка, оптическая ось () параллельна поверхности положительного кристалла.
Решение:
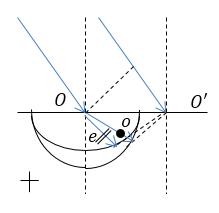
Рисунок 4.


















