В основе явления, на котором строится интерферометр Фабри - Перо лежит суперпозиция множества лучей с убывающей интенсивностью. Сам прибор состоит из двух кварцевых (стеклянных) пластинок, которые разделяет воздушный зазор (рис.1).
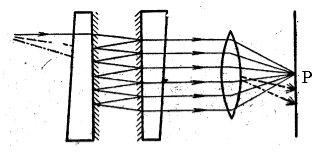
Рисунок 1.
Внутренние поверхности пластиной подвергают тщательной обработке, убирая все неровности, которые не должны быть больше чет сотые доли длины волны света. На подготовленные поверхности наносят полупрозрачные слои металла или пленки диэлектрика. Внешние поверхности пластинок делают немного непараллельными внутренним поверхностям, с целю не допустить бликования. В настоящее время пластинки закрепляют неподвижно. Внутренние поверхности пластинок выставляют строго параллельно, с неизменным расстоянием между ними. Такой интерферометр называют эталоном Фабри - Перо.
Допустим, что интенсивность луча, пришедшего в зазор между пластинами интерферометра равна $I_0$. В некоторой точке $А_1\ $этот луч частично выходит наружу (луч 1), частично отражается (луч $1'$) (рис.2). Интенсивность луча 1 будет равна:
где $\rho $ - коэффициент отражения поверхности пластинки, при этом интенсивность луча $1'$ ($I_1'$) можно определить как:
Далее луч $1'$ в точке $В_1$ делится на два луча (рис.2): луч $1'''$ далее участия в создании картины не принимает, отраженный луч $1''$ имеет интенсивность, равную:
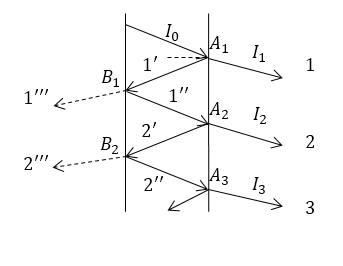
Рисунок 2.
В точке $А_2$ луч $1''$ снова делится на луч $2$, его интенсивность равна:
$I_2=\left(1-\rho \right)I''_1=\left(1-\rho \right){\rho }^2I_0\left(4\right)$и отраженный луч $2'$ и так далее. Интенсивность лучей 1,2, 3, ... находится в отношении:
Значит, амплитуды соотносятся как:
Надо отметить, что колебания в каждом из лучей 2,3,4,... отстает по фазе от колебания в предшествующем луче на величину $\delta $, которая определяется оптической разностью хода $\triangle $, которая появляется по пути луча, например: $A_1-B_1-A_2$. При этом можно сказать, что
где $\varphi $ - угол падения луча на поверхность отражения, $l$ - расстояние между пластинами.
Формула для расчета интенсивности
Если собрать полученные лучи 1,2,3 ... используя линзу, в точке $P$ (рис.1), интенсивность в этой точке будет определена как:
где $Ka^2=I_1$ - интенсивность первого луча (имеющего максимальную интенсивность), $a$ - постоянная амплитуда колебаний, $К$ - коэффициент пропорциональности между амплитудой колебаний и интенсивностью, $\rho $ - коэффициент отражения, величина $\delta $ равна:
Если через интерферометр проходит расходящийся пучок света, то в фокальной плоскости линзы появляются полосы равного наклона в виде колец.
Данный интерферометр применяют в спектроскопии, метрологии.
Разрешающая способность интерферометра
Разрешающая способность ($\epsilon$) интерферометра определяется минимальной разницей длин волн ($\triangle \lambda $) при которой возможно их разрешение:
Для интерферометра Фабри - Перо имеем:
Перечислите факторы, которые ограничивают разрешающую способность интерферометра Фабри - Перо.
Решение:
Согласно формуле для разрешающей способности интерферометра Фабри - Перо:
\[\epsilon=\frac{2\pi l}{\lambda }\frac{\sqrt{\rho }}{1-\rho }\left(1.1\right)\]можно добиться сколь угодно большой разрешающей способности прибора, достаточно сделать большим расстояние между пластинами ($l$) , а коэффициент отражения $\rho $ максимально приблизить к единице. Однако мешает этому ряд вещей, так:
- Пластины интерферометра не являются абсолютно плоскими. Их могут отполировать с точностью до $\frac{1}{200}$ длины волны, но не абсолютно ровно. Отклонение поверхности пластин от идеальной плоскости ведет к изменению $\delta $. Если изменение $\triangle l\approx \alpha \lambda $, где ($\alpha \ll 1$), изменение $\triangle \delta \approx 4\pi \alpha $. Причем должно выполняться условие:
-
Следующее ограничение вызвано необходимостью идеальной параллельности пластин. Точность параллельности такая же, как к идеальной плоскости.
-
Невозможно установить большое расстояние между пластинами, так как с увеличением расстояния радиус первого интерференционного кольца и расстояние между кольцами уменьшаются, это ухудшает условия анализа картины интерференции.
Опишите распределение интенсивности в интерференционной картине, получаемой с помощью интерферометра Фабри - Перо.
Решение:
Примем как основу для ответа на вопрос формулу для интенсивности, которая относится к заданному интерферометру:
\[I\left(\delta \right)=\frac{Ka^2}{{\left(1-\rho \right)}^2+4\rho \cdot {sin}^2\left(\frac{\delta }{2}\right)}=\frac{Ka^2}{1+\frac{4\rho \cdot {sin}^2\left(\frac{\delta }{2}\right)}{{\left(1-\rho \right)}^2}}\left(2.1\right)\]В случае, когда $\delta =2\pi m\ (m=1,2,\dots )$, получаем, что:
\[{sin}^2\left(\frac{\delta }{2}\right)=0\left(2.2\right).\]Следовательно, можно получить полное прохождение света ($I_{max}=Ka^2=I_0$). Причиной появления этого эффекта является то, что соседние волны, отражаемые от поверхностей, обладают около первой поверхности разностью фаз равной $\pi $, и взаимно ослабляются, как следствие - отсутствует отраженная волна. У второй поверхности разность волн, с минимальной разностью фаз, равна 2$\ \pi $. Данные волны усиливают друг друга, проходя через поверхность без ослабления.
При ${sin}^2\left(\frac{\delta }{2}\right)=1\ $или $\delta =\pi \left(2m+1\right)\left(m=1,2\dots \right),\ \ $интенсивность проходящего света минимальна:
\[I_{min}=\frac{Ka^2{\left(1-\rho \right)}^2}{{\left(1-\rho \right)}^2+4\rho }=\frac{Ka^2{\left(1-\rho \right)}^2}{{\left(1+\rho \right)}^2}\left(2.3\right).\]Если коэффициент отражения можно считать $\rho \approx 1$, то $I_{min}\approx 0.$ Это значит, что почти весь свет отражается. То есть, разность фаз между соседними волнами (имеющими наименьшую разность фаз), которые прошли через вторую поверхность, равна $\pi $, эти волны взаимно ослабляют друг друга, так прошедшая волна почти отсутствует.











