Рассмотрим интерференцию в плоскопараллельной пластине, будем учитывать лучи, которые претерпевают многократные отражения (рис.1). Пусть коэффициент отражения (доля энергии падающего света, которая возвращается в отраженном луче) света от границы пластинки с воздухом будет $\rho .$ Если поглощения энергии нет, то доля энергии, которая проходит через границу раздела равна $(1-\ \rho )$. В том случае, если по обе стороны пластинки воздух (одинаковая среда), то коэффициенты отражения одинаковы.
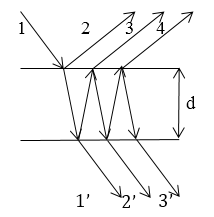
Рисунок 1.
Будем считать, что на пластинку падает монохроматический свет, его интенсивность равна $I_0$. В таком случае интенсивности пучков $1',2',3',\dots $ равны, соответственно:
При этом соответствующие вещественные амплитуды:
где $a_0$ - амплитуда падающей волны. Разность хода между двумя соседними интерферирующими пучками:
где $\varphi $ - угол падения луча на поверхность.
Разность фаз ($\delta $) при этом составит:
Амплитуду волны, которая прошла через пластинку можно представить как убывающую геометрическую прогрессию:
В том случае, если пластинка длинная, то прогрессию считаем бесконечной, следовательно:
Используя выражение (6) запишем формулу интенсивности прошедшей волны:
Найдем интенсивность отраженной волны ($I_r$). Интенсивности отраженных лучей (1,2,3,...) можно выразить как:
При этом соответственные вещественные амплитуды равны:
где минусы в формулах для амплитуд учитывают потерю половины волны при отражении от поверхности пластины. В данном случае луч $2$ отражается от границы воздух - пластина (стекло), все остальные отражения происходят на границе стекло - воздух. Суммарная амплитуда отраженной волны представлена геометрической прогрессией:
В таком случае выражение для интенсивности результирующей отраженной волны имеет вид:
Формулы (7) и (11) называются формулами Эйри.
Следствия из формул Эйри
Если мы считаем, что поглощения света средой не происходит, то выполняется равенство:
Картины распределения интенсивностей в прошедшем и отраженном свете являются взаимно дополняющими, что означает, что максимумам одной картины соответствуют минимумы другой. Для того чтобы получить интерференционную картину следует использовать длинный источник света. При этом полосы интерференции будут полосами равного наклона. Их можно собрать линзой на экран, который помещается в фокальную плоскость. Интерференционные полосы будут иметь вид концентрических колец, с центром в точке схождения лучей, перпендикулярных поверхности пластины.
Максимумы в проходящем свете получают при $\delta =2\pi m\ \left(где\ m - целое\ число\ \right).\ $В отраженном свете это условие минимума.
Многолучевая интерференция реализуется в толстых пластинах, следовательно, для того чтобы получить интерференционную картину надо использовать свет высокой монохроматичности. Методами интерференционной спектроскопии исследуют структуру тонких спектральных линий. Интерференционные спектроскопы имеют высокую разрешающую способность при простом устройстве, дешевизне и удобстве в применении.
Покажите, что из формул Эйри следует, что при отсутствии поглощения $I_0=I_r+I_l$.
Решение:
Запишем формулы Эйри интенсивности прошедшего света ($I_l$):
\[I_l=\frac{{\left(1-\rho \right)}^2}{{\left(1-\rho \right)}^2+4\rho {sin}^2\left(\frac{\delta }{2}\right)}I_0\left(1.1\right)\ и\]отраженного света:
\[I_r=\frac{4\rho {sin}^2\left(\frac{\delta }{2}\right)}{{\left(1-\rho \right)}^2+4\rho {sin}^2\left(\frac{\delta }{2}\right)}I_0\left(1.2\right).\]Проведем прямое суммирование данных выражений:
\[I_l+I_r=\frac{{\left(1-\rho \right)}^2}{{\left(1-\rho \right)}^2+4\rho {sin}^2\left(\frac{\delta }{2}\right)}I_0+\frac{4\rho {sin}^2\left(\frac{\delta }{2}\right)}{{\left(1-\rho \right)}^2+4\rho {sin}^2\left(\frac{\delta }{2}\right)}I_0=\frac{{\left(1-\rho \right)}^2+4\rho {sin}^2\left(\frac{\delta }{2}\right)}{{\left(1-\rho \right)}^2+4\rho {sin}^2\left(\frac{\delta }{2}\right)}I_0=I_0.\]Что и требовалось доказать.
Чем отличается распределение интенсивности при многолучевой интерференции, если показатель отражения очень мал ($\rho \ll 1$), и если он стремится к единице.
Решение:
Определим, каково распределение интенсивности при многолучевой интерференции света если коэффициент отражения очень мал. Запишем формулу Эйри для интенсивности прошедшего света ($I_l$):
\[I_l=\frac{{\left(1-\rho \right)}^2}{{\left(1-\rho \right)}^2+4\rho {sin}^2\left(\frac{\delta }{2}\right)}I_0\left(2.1\right)\ \]при $\rho \ll 1$ распределение интенсивности в прошедшей через пластинку волне, если пренебречь ${\rho }^2$, и сделать разложение по$\ \rho $ можно представить как:
\[I_l=1-4с{sin}^2\left(\frac{\delta}{2}\right)=1-2с\left(1-cos \delta \right)\left(2.2\right).\]Приведем формулу Эйри для интенсивности отраженного света:
\[I_r=\frac{4\rho {sin}^2\left(\frac{\delta }{2}\right)}{{\left(1-\rho \right)}^2+4\rho {sin}^2\left(\frac{\delta }{2}\right)}I_0\left(2.3\right).\]учитывая $\rho \ll 1,$ проведем операции аналогичные тем, что делали ранее, получим:
\[I_r=4\rho {sin}^2\left(\frac{\delta }{2}\right)=2\rho \left(1-cos\delta \right)\left(2.4\right).\]Распределение интенсивности определяют условия аналогичные условиям простой двухлучевой интерференции. Как будто не учитываются многократные отражения.
Распределение интенсивности сильно изменяется, если коэффициент отражения растет, особенно, если он близок к единице. В этом случае почти весь свет сосредоточен в узких интерференционных полосах на темном фоне. В отраженном свете, получаются такие же резкие темные полосы интерференционной картины. Числитель в формуле (2.1) - постоянен. В максимуме (при $\delta =2\pi m$) $I_{max}=I_0.$












