Разместим на пути распространения сферической волны света непрозрачную преграду (экран), в котором сделано круглое отверстие радиуса $r_0$. При этом экран располагается так, что перпендикуляр от источника света ($S$) попадает в центр отверстия (рис.1).
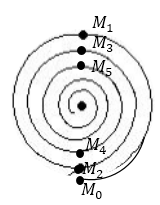
Рисунок 1.
В том случае, если $r_0\ll a,b$, то расстояние $a$ можно считать расстоянием от преграды до источника света, $b$ - расстояние от преграды до точки $A$. В том случае, если расстояния удовлетворяют выражению:
где $m$ - целое число, в таком случае отверстие открывает $m$ первых зон Френеля, построены для точки $A$. Соответственно можно выразить количество открытых зон Френеля как:
Амплитуду в точке $A$ найдем как:
где пред амплитудой стоит знак плюс для нечетных $m$. При этом величины амплитуд двух соседних зон почти одинаковы. Значит, можно записать:
Для небольших m $A_m\approx A_1$, получается, что при нечетных $m$ амплитуда в точке $A$ оказывается равной величине около $A_1$, при четных $m$ амплитуда равна нулю.
Если преграду убирают, то амплитуда в точке $A$ равна $\frac{A_1}{2}$. Следует сделать вывод о том, что преграда с отверстием, которое открывает малое число зон, ведет к росту амплитуды почти в два раза, интенсивности - в четыре раза.
Характер дифракционной картины
Рассмотрим, какова дифракционная картина на экране (рис.1). Ее вид зависит от количества зон Френеля, которые укладываются в отверстии. Отверстие на преграждающем экране расположено симметрично относительно прямой $SA$. Следовательно, освещенность различных точек демонстрационного экрана зависит только от расстояния до точки $A$. В точке $A$ интенсивность достигает максимума или минимума, что зависит от того четное или нечетное число зон Френеля открыто. Пусть количество открытых зон равно трем. В центре картины дифракции интенсивность имеет максимум. Картина зон Френеля для этой точки имеет вид рис.2 (а).
Рассмотрим точку $A'$. Картина зон Френеля для нее ограничена краями отверстия. Она изображена на рис.2 (б). Края отверстия прикроют часть третьей зоны, при этом фрагментарно откроется четвертая. В результате интенсивность света уменьшается и при некотором положении точки $A'$ станет минимальной.
В точке $A''$ края отверстия частично закроют третью и вторую зоны Френеля, при этом откроется часть пятой зоны (рис.2(в)). В сумме объем нечетных зон окажется выше, интенсивность в точке $A''$ достигает максимума, при этом слабее, чем в точке $A$.
Получается, что картина дифракции от круглого отверстия является совокупностью чередующихся светлых и темных концентрических колец. В центре этой картины или светлое, или темное пятно.
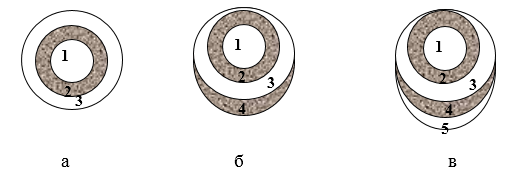
Рисунок 2.
Если демонстрационный экран перемещать параллельно самому себе по прямой $SA$, то темные и светлые полосы меняют друг друга, так как согласно формуле (2), если изменяется $b$, то $m$ может становиться то четным, то нечетным.
В том случае, если отверстие в преграде открывает только часть центральной зоны Френеля, то на экране мы имеем размытое светлое пятно (чередования максимумов и минимумов не возникает).
Если открыто большое количество зон Френеля, то чередование светлых и темных колец мы можем видеть только в узкой области на границе геометрической тени.
Если отверстие преграды освещено белым светом, то кольца окрашиваются.
Количество открытых зон Френеля зависит от диаметра отверстия. Если диаметр большой, то результирующая амплитуда такая же, как при полностью открытом фронте волны. Дифракции не наблюдается.
Задание: Каков радиус отверстия, если на экране наблюдается картина дифракции? Центр дифракционной картины является самым темным. Расстояние от дифракционной картины до точечного источника света равна $1 м$, $\lambda =0,5 мкм$. Диафрагма с круглым отверстием расположена посередине между источником и экраном.
Решение:
Как основу для решения задачи используем формулу:
\[r^2=\frac{ab}{a+b}m\lambda \left(1.1\right).\]По условию задачи имеем минимум интенсивности света в центре, это значит, что $m=2$. Формула (1.1) преобразуется к виду:
\[r=\sqrt{\frac{2ab}{a+b}\lambda }\left(1.2\right).\]Переведем длину волны в систему СИ: $\lambda =0,5\ мкм=0,5\cdot {10}^{-6}м.$ Проведем вычисления:
\[r=\sqrt{\frac{2\cdot 0,5\cdot 0,5}{0,5+0,5}\cdot 0,5\cdot {10}^{-6}}=0,5\cdot {10}^{-3}\left(м\right).\]Ответ: $r=0,5 мм$.
Задание: Параллельный пучок света нормально падает на экран с круглым отверстием. Радиус отверстия равен $r=1,5 \ мм$, $\lambda =0,5 \ мкм$. Расстояние от отверстия до точки наблюдения $b=1,5 \ м$ . Какое количество зон Френеля укладывается в отверстии? Максимум или минимум находится в центре дифракционной картины?
Решение:
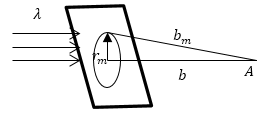
Рисунок 3.
Исходя из выражения, которое определяет зоны Френеля:
\[b_m=b+m\frac{\lambda }{2}(2.1)\]используя формулу для радиусов зон (рис.3):
\[{r_m}^2={b_m}^2-b^2\ \left(2.2\right)\]получим уравнение:
\[{r_m}^2={\left(b+m\frac{\lambda}{2}\right)}^2-b^2=b^2+2bm\frac{\lambda}{2}+{\left(m\frac{\lambda}{2}\right)}^2-b^2=bm\lambda +{\left(m\frac{\lambda}{2}\right)}^2\left(2.3\right).\]Так как длина волны видимого света мала, то ее квадратами можно пренебречь, то есть получаем:
\[{r_m}^2\approx bm\lambda \to r=\sqrt{bm\lambda }\left(2.4\right).\]Из выражения (2.4) получим $m$:
\[m=\frac{r^2}{b\lambda }\left(2.5\right).\]Проведем расчет, если получим $m$ - четное число, то имеем минимум, если $m$ равно нечетному числу, то максимум.$\ $
\[m=\frac{{(1,5\cdot {10}^{-3})}^2}{1,5\cdot 0,5\cdot {10}^{-6}}=3\]Ответ: В отверстии укладывается 3 зоны Френеля. В центре картины дифракции имеется светлое пятно.











