Дифракционная теория формирования изображений

Основная задача теории создания изображения -- описание распространения волн света от предмета до изображения сквозь оптическую систему. При этом фронт волны, который исходит от точки предмета, терпит преломление или отражение на оптических поверхностях, после этого сходится к точке изображения. В ходе подобных преобразований форма волнового фронта нарушается, что проявляется в изменении фазу поля. Помимо этого, фронт волны ограничивается диафрагмами (отверстиями) на которых поле дифрагирует. При этом в ходе распространения волны сквозь вещество интенсивность света уменьшается. Уравнение Гельмгольца для комплексной амплитуды при этом запишется как:

где $N\left(\overrightarrow{r}\right)$ -- функция, которая описывает воздействие оптической системы на комплексную амплитуду поля волны света. Она описывает оптические среды, форму и местоположение поверхностей отражения и преломления, диафрагмы и отверстия (в виде граничных условий). Частное решение уравнения (1), которое соответствует заданной функции $N\left(\overrightarrow{r}\right)$ и амплитуде поля на поверхности предмета описывает поле в любой точке пространства в пространстве между предметом и его изображением. Но получить такое решение для произвольной системы не представляется возможным, а решение для частного случая не дает возможности сделать обобщения. Так, прохождение волны сквозь произвольную оптическую систему описывают с использованием частных решений уравнения Гельмгольца, которые получают, используя приближения и допущения.

В случае распространении волны сквозь оптическую систему, определяющую роль будут играть явления дифракции. Данное явление имеет место на диафрагмах, которые чаще всего, являются отверстиями круглой или прямоугольной формы. Применение теории дифракции дает возможность описать прохождение поля световой волны от объекта до его образа сквозь оптическую систему и создать соответствующую модель формирования изображения.

Пусть поверхности $S_A\ и\ S_B$ разделяет оптическая система (последовательностью оптических поверхностей: $S_1,\dots \ \ S_i$), между ними вещества имеют показатели преломления равные: $n_1,\dots \ \ n_{i-1}.$ Допустим, что поверхности $S_1,\dots \ \ S_i$ гладкие, показатели преломления постоянны (изменяются плавно), тогда дифракцией на неровностях поверхностей и неоднородностях $n_1,\dots \ \ n_{i-1}$, можно пренебречь. Будем считать, что поверхности $S_A\ и\ S_B$ не являются сопряженными оптически (имеется не больше одного луча, который соединяет две точки этих поверхностей) (рис.1).

Общее выражение, которое описывает дифракцию при распространении волны света через оптическую систему можно записать как:

где $K\left(\overrightarrow{r_A,}\overrightarrow{r_B}\right)=cos (\alpha )\sqrt{d\Omega {\cdot n}^2/dS_B cos (\alpha ')}$, $cos\alpha $ -- проекция орта луча $\overrightarrow{q}$ на нормаль к поверхности $S_A.\ d\Omega $ -- элементарный телесный угол лучевой трубки, который выходит из точки А. $\tau \left(\overrightarrow{r_A,}\overrightarrow{r_B}\right)$ -- коэффициент энергетического пропускания. Расстояние между точками А и В заменяется на оптический путь между этими точками, то есть координатный эйконал $E\left(\overrightarrow{r_A,}\overrightarrow{r_B}\right).$

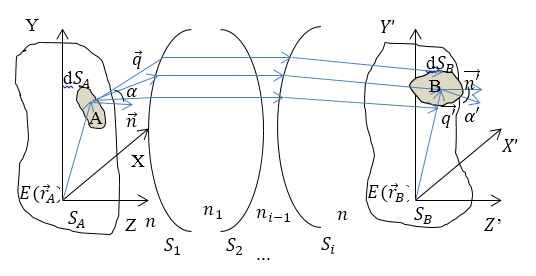
Рисунок 1.

Если коэффициент комплексного пропускания оптической системы записывают как:

то распространение волны в оптической системе, учитывая дифракцию, записывается как:

Модель, которая описывает формирование изображения, должна учесть работу всех диафрагм, линз и описывать распространение поля как последовательность дифракций на каждой диафрагме и оправе. Создание подобной модели весьма сложно и ненужно. Используются упрощенные модели, в которых дифракция учитывается на одной диафрагме.

Модель Аббе

Одну из моделей действия оптической системы при создании изображения сделал Аббе. Он использовал волновую теорию света при этом. Ученый сделал модель создания изображения с двойной дифракцией.

В соответствии с моделью Аббе предмет ведет себя как дифракционная решетка, следовательно, когда проводится анализ формирования изображения необходимо исследовать распространение дифрагированного поля от предмета до задней фокальной плоскости объектива. При этом картина дифракции в данной плоскости является спектром плоских волн. На следующем этапе (при использовании приближения Фраунгофера) исследуется распространение поля от фокальной плоскости до плоскости образа.

Данная модель имеет недостатки, так как не учитывает того, как влияет оптическая система на амплитуду и фазу распространяющихся волн, описывая преобразование поля между поверхностями объекта и его изображения. Кроме того существует необходимость учитывать ограничение размеров фронта волны, которая распространяется чрез оптическую систему.