Дифракционная картина в дальней зоне как Фурье-образ дифракционного объекта

Реализация Фурье - образа

Если световая волна $E_0$ распространяется по оси $Z$ и попадает на экран, который совпадает с плоскостью $z=0$. При этом амплитудный коэффициент пропускания экрана равен $\tau \left(x,y\right).\ $В таком случае сразу за экраном поле волны, которая прошла через преграду ($E_{\tau }$) равно:

При этом в соответствии с теоремой Фурье функция $E_{\tau }\left(x,y\right)$ представляется как:

Выражение (2) обозначает, что световое поле представлено как суперпозиция плоских волн, чьи амплитуды обозначены $F\left(u,v\right)-пространственный\ спектр$. Данные амплитуды определяются пространственным преобразованием Фурье вида:

где $u=\frac{cos\alpha }{\lambda }$, $v=\frac{cos\beta }{\lambda }$, ($\alpha \ и\ \beta$ -- углы между волновым вектором и соответствующими осями $X$ и $Y$) -- пространственные угловые частоты. Данные частоты определяют количество периодов колебания на единицу длины вдоль соответствующей оси. Кроме того пространственные частоты задают направление распространения плоской волны. Следует заметить, что выполняется равенство:

для направляющих косинусов любого вектора.

Получается, что если световая волна дифрагирует на относительно большие углы (относительно оси $Z$), то излучение содержит высокие пространственные частоты. И наоборот. Если волна распространяется по оси $Z$, то ей соответствует нулевая пространственная частота. Получается, что для того чтобы решить задачу Фраунгофера достаточно найти пространственный спектр волнового поля за экраном, который определен уравнением (1) и равен свертке спектров падающей волны $E_0\left(x,y\right)\ $и коэффициента пропускания экрана. Если $E_0\left(x,y\right)$ является плоской волной, ее поле не зависит от поперечных координат, угловой спектр совпадет с угловым спектром пропускания экрана.

Картина дифракции Фраунгофера -- Фурье образ

Дифракцию Фраунгофера можно наблюдать, если выполняется условие для дальней зоны в фокальной плоскости оптической системы:

где $l$ -- расстояние от препятствия (отверстия) до экрана, $b$ -- ширина щели (диаметр/радиус).

Рассмотрим плоскость $P$, которой принадлежит излучающая поверхность $S$, плоскость наблюдения при этом будет $P'$. Расстояние между этими плоскостями равно $z$ (рис.1).

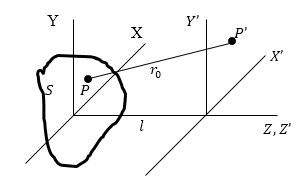
Рисунок 1.

Допустим, что вне излучающей поверхности $E\left(x,y\right)=0$, причем размеры $S$ много меньше, чем расстояние $l$.

В таком случае расстояние $r_0$ можно представить как:

Для $E(P')$ можно записать выражение:

Если расстояние $l$ велико ($l\gg k\frac{x^2+y^2}{2}$) то выражение (7) преобразуется к виду:

Выражение (8) с фурье -- образ распределения поля на поверхности S для функций пространственных частот $u$ и $v$, которые равны:

Надо отметить, что для дифракции Фраунгофера нет комплексного коэффициента усиления, так как нарушено условие пространственной инвариантности поля.

Примеры Фурье-образов