Дифракционная решетка -- прибор, который осуществляет периодическую модуляцию падающей волны света по амплитуде и фазе.
Амплитудные дифракционные решетки
Пусть одномерная амплитудная решетка состоит из $N$ параллельных щелей (ширина щели $b$) и затемненных промежутков. При этом $d$ - период решетки (рис.1).
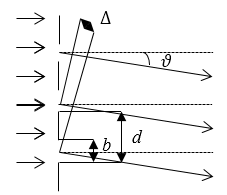
Рисунок 1.
Если свет падает на амплитудную решетку нормально, то разность хода ($\triangle $) монохромного света волн, которые испускаются соседними щелями равна:
При этом фазовый сдвиг ($\delta $) равен:
где $u=\frac{sin\vartheta }{\lambda }$ -- пространственная частота. Результирующую амплитуду при этом найдем как сумму геометрической прогрессии:
где $E_1$ -- амплитуда поля, после прохождения одной щели. Выражение для интенсивности света, прошедшего через амплитудную дифракционную решетку при этом примет вид:
где $I_0$ -- интенсивность падающего света, $I_1$ - интенсивность света, прошедшего через одну щель. $I_N$ -- интенсивность света при многолучевой интерференции. В данном случае все пучки света имеют равную интенсивность.
Числитель и знаменатель функции $I_N\ \ $равен нулю при выполнении условия главных максимумов:
Учитывая, что:
значит:
Так, при выполнении условия главных максимумов (5), интенсивность света, который совершил дифракцию на решетке из $N$ щелей, увеличивается в $N^2$ раз. Такая зависимость определена многолучевой интерференцией пучков света, которые прошли через регулярную структуру. Из формулы (7) следует, что интенсивность главных максимумов быстро убывает с ростом порядка. Кроме того, данная интенсивность зависит от отношения $\frac{d}{b}$- целое число. Главные максимумы порядков $\frac{d}{b}$, 2$\frac{d}{b}$, ..., приходятся на минимумы дифракции на одной щели, и их интенсивность оказывается равной нулю. Так, при $\frac{d}{b}=2$ прозрачная и непрозрачная части равны друг другу, спектр решетки имеет только главные максимумы нулевого и нечетных порядков, четных порядков нет.
Решетка из $N$ щелей создает в промежутках между главными максимумами ($N-1$) минимум освещенности и ($N-2$) побочных максимума. С увеличением $N$ относительная интенсивность дополнительных максимумов существенно падает и их существованием можно пренебречь.
В случае наклонного падения света на решетку отличной от нуля является пространственная частота:
В таком случае в условие главных максимумов войдет разность пространственных частот:
Пространственный спектр дифракционной решетки образуется в соответствии с принципами Фурье -- преобразования.
Характеристиками спектральных свойств дифракционной решетки являются:
-
Угловая дисперсия ($D$):
\[D=\frac{m}{dcos\vartheta }\left(10\right).\] -
Разрешающая способность ($R$):
\[R=\frac{\lambda }{\triangle \lambda }=mN\left(11\right).\] -
Свободная дисперсионная область $G$ -- величина, определяющая для спектра диапазон, который свободен от перекрытия спектров:
\[G=\frac{\lambda }{m}\left(12\right).\]
Для практического применения амплитудные дифракционные решетки имеют характеристики невыгодные. Свет разбрасывается ими по многим порядкам, причем основная часть энергии приходится на ахроматический нулевой порядок. При этом в максимумы высоких порядков, которые имеют высокую дисперсию и разрешающий порядок попадает мало света.
Фазовые дифракционные решетки
Фазовые дифракционные решетки имеют лучшие спектральные свойства. Штрихи таких решеток имеют определенный профиль (рис.2). Фазовые дифракционные решетки бывают отражательными (рис.2) или прозрачными.
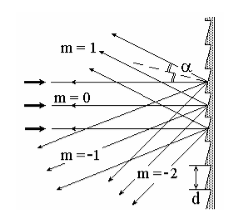
Рисунок 2.
Эти решетки почти не влияют на амплитуду световой волны, но вносят периодические изменения в ее фазу. Если мы имеем отражательную решетку (рис.2) с профилированным штрихом, то ее максимальная интенсивность света, прошедшего дифракцию, может наблюдаться в направлении зеркального отражения от плоскости штриха ($m=1$). В том случае, если ширина рабочей грани занимает около периода ($b\approx d$) и $2sin\alpha =\frac{m\lambda }{d}$ решетка выдает только один главный максимум порядка $m$. Угол $\alpha $ при этом условии называется углом блеска.
Для того чтобы максимум энергии направлялся в первый порядок прозрачной фазовой решетки надо, чтобы выполнялись для угла отклонения $\vartheta_0\ $сразу два условия:
где $n$ -- показатель преломления материала решетки, $\alpha $ -- угол при вершине микро призмы.
Задание: Объясните, чем характеризуется разрешающая способность дифракционной решетки?
Решение:
Разрешающая способность ($R$) дифракционной решетки определена как:
\[R=\frac{\lambda }{\triangle \lambda }=mN\left(1.1\right).\]Для дифракционной решетки, которая имеет большое количество (около десятков тысяч) штрихов ($N$) разрешающая способность велика. Для увеличения разрешающей способности дифракционной решетки следует увеличить $m$ (порядки интерференции). Но величины $m$ ограничены углами отклонения $\vartheta \le \frac{\pi }{2}$ и, значит $sin\vartheta $ в выражении:
\[dsin\vartheta =m\lambda \ (m=0,\pm 1,\pm 2,\dots (1.2))\]не может быть больше единицы. Получается, что:
\[m_{max}=\frac{d}{\lambda }\left(1.3\right).\]Получаем:
\[R_{max}=\frac{d}{\lambda }N(1.4).\]Кроме того, решетка с большим, $N$ имеют лучшую угловую дисперсию:
\[R=\frac{\delta \vartheta }{\delta \lambda }\left(1.5\right).\]Из (1.2) имеем:
\[dcos\vartheta \delta \vartheta =m\delta \lambda \left(1.6\right).\]Соответственно:
\[R=\frac{m}{dcos\vartheta }\left(1.7\right).\]Выражение (1.7) означает, что при малых $d$ угловая дисперсия выше, при малых $m$. Практическое значение имеют дисперсионные решетки с большим $N$ и большой общей шириной.
Задание: Чем (с точки зрения картины интерференции), отличается фазовая дифракционная решетка?
Решение:
Общий характер интерференционной картины такой решетки неизменен, меняется только распределение интенсивности, при этом максимальная интенсивность находится не в главном максимуме на угле $\vartheta =0$, а на том максимуме, который попадает на угол $\vartheta =(n-1)\alpha $, или находится около данного угла. Что позволяет работать с высокими порядками интерференции ($m$), что улучшает разрешающую способность дифракционной решетки при уменьшении потерь в интенсивности.











