
Параметры состояния связаны друг с другом. Соотношение, которое определяет эту связь, называется уравнением состояния этого тела. В простейшем случае равновесное состояние тела определяется значением тех параметров: давления p, объема V и температуры, массу тела (системы) обычно считают известной. Аналитически связь между этими параметрами выражают как функцию F:
Уравнение (1) называют при этом уравнением состояния. Это закон, который описывает характер изменения свойств вещества при изменении внешних условий.
Что такое идеальный газ
Особенно простым, но весьма информативным является уравнение состояния так называемого идеального газа.
Идеальным называют газ, в котором взаимодействием молекул между собой можно пренебречь.
К идеальным можно отнести разреженные газы. Особенно близки по своему поведению к идеальному газу гелий и водород. Идеальный газ представляет собой упрощенную математическую модель реального газа: молекулы считаются движущимися хаотически, а соударения между молекулами и удары молекул о стенки сосуда --- упругими, такими, которые не приводя к потерям энергии в системе. Такая упрощенная модель очень удобна, так как не требует учитывать силы взаимодействия между молекулами газа. Большинство реальных газов не отличаются в своем поведении от идеального газа при условиях, когда суммарный объем молекул пренебрежимо мал по сравнению с объемом сосуда (т.е. при атмосферном давлении и комнатной температуре), что позволяет использовать уравнение состояния идеального газа в сложных расчетах.
Уравнение состояния идеального газа можно записать в нескольких видах (2), (3), (5):
\[pV=\frac{m}{\mu }RT=\nu RT\ (2)\]Уравнение (2) -- уравнение Менделеева -- Клайперона, где m - масса газа, $\mu $ -- молярная масса газа, $R=8,31\ \frac{Дж}{моль\cdot К}$- универсальная газовая постоянная, $\nu \ $- количество молей вещества.
\[pV=NkT\ \left(3\right),\]где N - число молекул газа в массе m, $k=1,38\cdot 10^{-23}\frac{Дж}{К}$, постоянная Больцмана, которая определяет «долю» газовой постоянной приходящуюся на одну молекулу и
\[N=\frac{mN_A}{\mu }\ (4),\ \]$N_A=6,02\cdot 10^{23}моль^{-1}$ -- постоянная Авогадро.
Если разделить в (4) обе части на V, то получим следующую форму записи уравнения состояния идеального газа:
\[p=nkT\ \left(5\right),\]где $n=\frac{N}{V}$- число частиц в единице объема или концентрация частиц.
Что такое реальный газ
Обратимся теперь к более сложным системам - к неидеальным газам и жидкостям.
Реальным газом называют газ, между молекулами которого существуют заметные силы взаимодействия.
В неидеальных, плотных газах взаимодействие молекул велико и его нужно учитывать. Оказывается, что взаимодействие молекул столь сильно усложняет физическую картину, что точное уравнение состояния неидеального газа не удается записать в простой форме. В таком случае прибегают к приближенным формулам, найденным полуэмпирический. Наиболее удачной такой формулой является уравнение Ван-деp-Ваальса.
Взаимодействие молекул имеет сложный характер. На сравнительно больших расстояниях между молекулами действуют силы притяжения. По мере уменьшения расстояния силы притяжения сначала растут, но затем уменьшаются и переходят в силы отталкивания. Притяжение и отталкивание молекул можно рассматривать и учитывать раздельно. Уравнение Ван-дер-Ваальса описывающее состояние одного моля реального газа:
\[\left(p+\frac{a}{V^2_{\mu }}\right)\left(V_{\mu }-b\right)=RT\ \left(6\right),\]где $\frac{a}{V^2_{\mu }}$- внутреннее давление, обусловленное силами притяжения между молекулами, b -- поправка на собственный объем молекул, которая учитывает действие сил отталкивания между молекулами, причем
\[b=N_A\frac{2}{3}\pi d^3(7),\]где d - диаметр молекулы,
величина a вычисляется по формуле:
\[a=-2\pi N^2_A\int\nolimits^{\infty }_d{W_p\left(r\right)r^2dr\ \left(8\right),}\]где $W_p\left(r\right)\ $- потенциальная энергия притяжения двух молекул.
С увеличением объема роль поправок в уравнении (6) становится менее существенной. И в пределе уравнение (6) переходит в уравнение (2). Это согласуется с тем фактом, что при уменьшении плотности реальные газы по своим свойствам приближаются к идеальным.
Достоинством уравнения Ван-деp-Ваальса является то обстоятельство, что оно при очень больших плотностях приближённо описывает и свойства жидкости, в частности плохую ее сжимаемость. Поэтому есть основание полагать, что уравнение Ван-деp-Ваальса позволит отразить и переход от жидкости к газу (или от газа к жидкости).
На рис.1 изображена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T, построенная из соответствующего уравнения.
В области "извилины" (участок КМ) изотерма трижды пересекает изобару. На участке [$V_1$, $V_2$] давление pастет с увеличением объема.
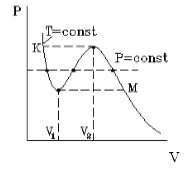
рис.1
Такая зависимость невозможна. Это может означать, что в данной области с веществом пpоисходит что-то необычное. Что именно это, невозможно увидеть из уравнения Ван-деp-Ваальса. Необходимо обратиться к опыту. Опыт показывает, что в области "извилины" на изотерме в состоянии равновесия вещество расслаивается на две фазы: на жидкую и газообразную. Обе фазы сосуществуют одновременно и находятся в фазовом равновесии. В фазовом равновесии протекают процессы испарения жидкости и конденсации газа. Они идут с такой интенсивностью, что полностью компенсируют друг друга: количество жидкости и газа с течением времени остается неизменным. Газ, находящийся в фазовом равновесии со своей жидкостью, называется насыщенным паром. Если фазового равновесия нет, нет компенсации испарения и конденсации, то газ называется ненасыщенным паром. Как же ведет себя изотерма в области двухфазного состояния вещества (в области "извилины" изотермы Ван-деp-Ваальса)? Опыт показывает, что в этой области при изменении объема давление остается постоянным. График изотермы идет параллельно оси V(рис 2).
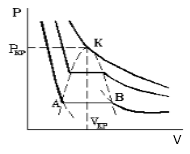
рис.2
По мере увеличения температуры участок двухфазных состояний на изотермах сужается, пока не превратится в точку (рис. 2). Это особая точка К, в которой исчезает различие между жидкостью и паром. Она называется критической точкой. Параметры, соответствующие критическому состоянию, называются критическими (критическая температура, критическое давление, критическая плотность вещества).
Задание: В процессе, который представлен на рисунке (рис.3) давление $p\sim T^n.\ $ Найти значение n.
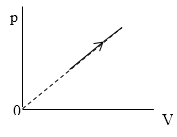
рис.3
Решение:
Из графика, который приведен на рис. 3 запишем уравнение процесса в параметрах p(V):
\[p=kV\ или\ p\sim V\ (1.1)\]Из уравнения Менделеева-Клайперона имеем:
\[pV\sim T\ (1.2)\]Используем (1.1), подставим вместо объема, получим:
\[p^2\sim T\to p\sim \sqrt{T\ }\left(1.3\right)\]Ответ: $n=1/2$.
Задание: Моль кислорода охлаждают до $-100^oС$. Определить давление, оказываемое газом на стенки сосуда, если занимаемый газом объем V = 0,1 л. Сравнить p с давлением идеального газа pid, если бы кислород вел себя как идеальный газ. Значения постоянных Ван-дер-Ваальса a и b, для кислорода $a=0,1358Па \cdot м^6/моль^2, b=3,167 \cdot 10^{-5}м^3/моль$
Решение: Из уравнения Ван-Дер-Ваальса следует, что:
\[p=\frac{RT}{V_{\mu }-b}-\frac{a}{V^{2\ }_{\mu }}(2.1)\]Переведем температуру в СИ: T=t+273, По условию $T=173K, V = 0,1 л=10^{-4}м^3$
Проведем расчет: $p=\frac{8,31\cdot 173}{\left(10-3,2\right)\cdot 10^{-5}}-\frac{0,1358}{({10}^{-4})^2}=75,61\cdot 10^5\left(Па\right)$
Для идеального газа:
\[p_{id}=\frac{\nu RT}{V}(2.2)\]Проведем расчет: $p_{id}=\frac{1\cdot 8,31\cdot 173}{{10}^{-4}}=143\cdot 10^5\ \left(Па\right)\left(2.3\right)$
Ответ: $p\approx 0,53p_{id}$










