В газе молекулы свободно движутся. Сталкиваются периодически между собой. Между двумя последовательными соударениями молекула движется равномерно и прямолинейно. Определим среднее количество столкновений молекулы газа с другими молекулами на время t=1с. Обозначим через $\left\langle dS\right\rangle $ элементарный средний путь, пройденный молекулой, считаем, что молекула двигалась прямолинейно со средней скоростью $\left\langle \overrightarrow{v}\right\rangle $. Будем считать, что газ идеальный, то есть его молекулы представляют собой твердые сферы диаметром d (это так называемый эффективный диаметр молекулы). Тогда число столкновений (z) молекулы с другими за t=1с будет равно количеству молекул, центры которых находятся в цилиндре (рис. 1), высота цилиндра $\left\langle \overrightarrow{v}\right\rangle t$, и диаметром d:
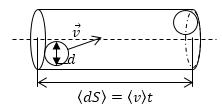
Рис. 1
Скорость - вектор, используем относительную среднюю скорость, зная, что
подставим в (1) вместо $\left\langle v\right\rangle :$
Расстояние, которое проходит молекула между двумя последовательными столкновениями, называется длинной свободного пробега ($\lambda $):
где $\sigma$- эффективное поперечное сечение соударения. Из выражения (4) видно, что средняя длина свободного пробега молекулы не зависит о температуры. Длина свободного пробега молекулы весьма важная физическая величина в МКТ. Используя ее, рассчитываются коэффициенты переноса.
Давление газа на стенки сосуда
Молекулы газа сталкиваются не только друг с другом, но и со стенками сосуда, в котором находится газ. Движущиеся молекулы газа обладают импульсом, сталкиваясь со стенками сосуда, молекулы передают свой импульс препятствию. Этим и обусловлено давление газа на стенки сосуда. Если мы рассматриваем идеальный газ, то считаем соударения молекул абсолютно упругими. Пусть газ находится в состоянии равновесия. Определим связь между давлением газа и скоростью отдельных его молекул. Известно, что $p={\frac{\triangle F_n}{\triangle S} ,\ \ }$ давление газа есть сила, действующая на единичную площадку поверхности сосуда. Сила, есть импульс, которые передают молекулы в единицу времени стенке сосуда ($\triangle \overrightarrow{F}=\frac{\triangle \overrightarrow{p}}{\triangle t}$). Найдем импульс. Молекула, ударяясь о стеку сосуда, отскакивает от нее, причем угол падения равен углу отражения (рис.2). Тогда стенке передается только $p_x,$ и $\triangle p_x=mv_x-(-mv_x)$=2$\ mv_x$
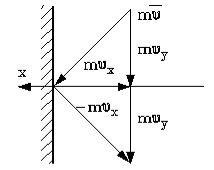
Рис. 2
Количество молекул, которые ударяются о единичную площадку стенки сосуда с газом, определяется по формуле:
Импульс, который получает стенка в этом случае, равен:
\[\triangle p_x=z\cdot 2\ mv_x=2\ m{v_x}^2\cdot n_0\cdot t\left(6\right),\]$n_0$ -- количество молекул, которые обладают скоростью $v_x$ и находятся в единице объема газа.
Полный импульс
При этом полный импульс, который получает стенка, равен сумме:
\[\triangle p=\sum\limits_{v_x>0}{2\ m{v_x}^2\cdot n_0\cdot \triangle t}\ \left(7\right).\]Умножим и разделим (7) на $\frac{n}{2}$, здесь n -- концентрация молекул в газе:
\[\triangle p=\sum\limits_{v_x>0}{\frac{2\ m{v_x}^2\cdot n_0\cdot \triangle t}{\frac{n}{2}}}\cdot \frac{n}{2}\left(8\right).\] \[\sum\limits_{v_x>0}{\frac{{v_x}^2\cdot n_0\cdot }{\frac{n}{2}}}=\left\langle {v_x}^2\right\rangle \to \triangle p=\frac{m\left\langle {v_x}^2\right\rangle \triangle tn}{2}\to F=\frac{\triangle p}{\triangle t}=\frac{m\left\langle {v_x}^2\right\rangle n}{2}\to p=\frac{m\left\langle {v_x}^2\right\rangle n}{2}\left(9\right).\]Напомню, что мы рассматривали единичную площадку.
Считая, что газ изотропен, имеем:
\[\left\langle v^2\right\rangle =\left\langle {v_x}^2\right\rangle +\left\langle {v_y}^2\right\rangle +\left\langle {v_z}^2\right\rangle =3\left\langle {v_x}^2\right\rangle \left(10\right)\]Следовательно, связь между давлением, скоростью отдельной молекулы и ее массы имеет вид:
\[p=\frac{2m\left\langle v^2\right\rangle n}{3\cdot 2}=\frac{2}{3}n\left\langle E_k\right\rangle \left(11\right).\]Уравнение (11) доказывает, что давление газа -- следствие действия отдельных молекул, и оно пропорционально средней кинетической энергии поступательного движения молекул.
Задание: При атмосферном давлении и температуре $t=0^oС$ длина свободного пробега молекулы водорода равна 0,1 мк.м. Оцените диаметр этой молекулы.
Решение:
Диаметр молекулы можно оценить, зная длину свободного пробега молекулы, так как:
\[\lambda =\frac{1}{\sqrt{2}\pi d^2\cdot n}\ \left(1.1\right)\]Концентрацию молекул водорода можно найти из условий задачи, используя уравнение состояния идеального газа (водород при атмосферном давлении и заданной температуре можно считать идеальным газам):
\[p=nkT\to n=\frac{p}{kT}\left(1.2\right).\]Подставим (1.2) в (1.1), получим:
\[\lambda =\frac{kT}{\sqrt{2}\pi d^2\cdot p}\to d=\sqrt{\frac{kT}{\lambda p\sqrt{2}\pi }}\left(1.3\right)\]Проведем расчёты, зная, что атмосферное давление это $p\approx 10^5Па,\ \lambda =0,1\ мк.м=10^{-7}м,\ t=0^0С\to T=273K\ \ $:
\[d=\sqrt{\frac{1,38\cdot 10^{-23}273}{\sqrt{2}\cdot 3,14\cdot 10^5\cdot 10^{-7}}}=\sqrt{8,5\cdot 10^{-20}}=2,3\cdot 10^{-10}(м)\]Ответ: Диаметр молекулы водорода порядка $2,3\cdot 10^{-10}м.$
Задание: Можно ли вычислить среднюю квадратичную скорость молекулы по заданным: средней энергии поступательного движения молекул$-\ \left\langle E_k\right\rangle \ $и молярной массе газа $\mu \sigma$
Решение:
В качестве основы для решения используем уравнение:
\[p=\frac{m\left\langle v^2\right\rangle n}{3}=\frac{2}{3}n\left\langle E_k\right\rangle \ \to \left\langle v^2\right\rangle =\frac{2\left\langle E_k\right\rangle }{m}\left(2.1\right),\]здесь $m$- масса одной молекулы, а мы знаем, что:
\[\frac{m}{\mu }=\frac{1}{N_A}\to m=\frac{\mu }{N_A}\to \left\langle v^2\right\rangle =\frac{2\left\langle E_k\right\rangle N_A}{\mu }.\]$N_A$- число Авогадро, величина известная.
Ответ: По заданным параметрам среднеквадратичную скорость вычислить можно, используя формулу: $\left\langle v_{kv}\right\rangle =\sqrt{\frac{2\left\langle E_k\right\rangle N_A}{\mu }}$.












