Различают следующие скорости, характеризующие движение молекул.
Средняя скорость движения молекул
средняя скорость движения молекул $\left\langle v\right\rangle $, которая определяется как:
где N -- число молекул. Или, среднюю скорость можно найти как:
где $F\left(v\right)=4\pi {\left(\frac{m_0}{2\pi kT}\right)}^{\frac{3}{2}}exp\left(-\frac{m_0v^2}{2kT}\right)v^2$ -- функция распределения молекул по модулю скорости, указывающая долю молекул со скоростями, находящимися в единичном интервале $dv$ около величины скорости $v$, $m_0$- масса молекулы, $k$- постоянная Болцмана, T -- термодинамическая температура. Для того, чтобы определить, как средняя скорость молекулы связана с макропараметрами газа, как системы частиц, найдем значение интеграла (2).
Произведем замену:
Следовательно:
Подставим (4) и (5) в (3), получим:
Проведем интегрирование по частям, получим:
где R -- универсальная газовая постоянная, $\mu $- молярная масса газа.
Среднюю скорость движения молекул называют также скоростью теплового движения молекул.
Средняя относительная скорость молекул:
\[\left\langle v_{otn}\right\rangle =\sqrt{2}\sqrt{\frac{8kT}{\pi m_0}}=\sqrt{2}\left\langle v\right\rangle \left(7\right).\]Средней квадратичной скоростью движения молекул газа называют величину:
\[\left\langle v_{kv}\right\rangle =\sqrt{\frac{1}{N}\sum\limits^N_{i=1}{{v_i}^2}}\left(8\right).\]Или
\[{\left\langle v_{kv}\right\rangle }^2=\int\nolimits^{\infty }_0{v^2F\left(v\right)dv\ \left(9\right).}\]Проводя интегрирование, которое аналогично интегрированию при получении связи средней скорости с температурой газа, получим:
\[\left\langle v_{kv}\right\rangle =\sqrt{\frac{3kT}{m_0}}=\sqrt{\frac{3RT}{\mu }}\left(10\right).\]Именно средняя квадратичная скорость поступательного движения молекул газа входит в основное уравнение молекулярно-кинетической теории:
\[p=\frac{1}{3}nm_0{\left\langle v_{kv}\right\rangle }^2\left(11\right),\]где $n=\frac{N}{V}$ -- концентрация частиц вещества, $N$- число частиц вещества, V- объем.
Задание: Определите, как изменяется средняя скорость движения молекул идеального газа при увеличении давления в процессе, представленном на графике (рис.1).
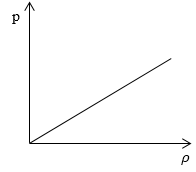
Рис. 1
Решение:
Запишем выражение для средней скорости движения молекул газа в виде:
\[\left\langle v\right\rangle =\sqrt{\frac{8kT}{\pi m_0}}\ \left(1.1\right)\]По графику видим, что $p\sim \rho \ или\ p=C\rho ,\ $ где C- некоторая константа.
\[m_0=\frac{\rho }{n},\ p=nkT=C\rho \to kT=\frac{C\rho }{n}\ \left(1.2\right).\]Подставим (1.2) в (1.1), получим:
\[\left\langle v\right\rangle =\sqrt{\frac{8kT}{\pi m_0}}=\sqrt{\frac{8C\rho }{\pi n}\frac{n}{\rho }}=\sqrt{\frac{8C}{\pi }}\left(1.3\right)\]Ответ: В процессе, изображенном на графике, с ростом давления средняя скорость движения молекул не изменяется.
Задание: Можно ли вычислить среднюю квадратичную скорость молекулы идеального газа, если известны: давление газа (p), молярная масса газа ($\mu $) и концентрация молекул газа (n)?
Решение:
Используем выражение для $\left\langle v_{kv}\right\rangle :$
\[\left\langle v_{kv}\right\rangle =\sqrt{\frac{3RT}{\mu }}\left(2.1\right).\]Кроме того, из уравнения Менделеева -- Клайперона и зная, что $\frac{m}{\mu }=\frac{N}{N_A}$:
\[pV=\frac{m}{\mu }RT=\frac{N}{N_A}RT\left(2.2\right).\]Разделим правую и левую части (2.2) на V, зная, что $\frac{N}{V}=n$ получим:
\[p=\frac{n}{N_A}RT\to RT=\frac{pN_A}{n}\ \left(2.3\right).\]Подставим (2.3) в выражение для среднеквадратичной скорости (2.1), имеем:
\[\left\langle v_{kv}\right\rangle =\sqrt{\frac{3pN_A}{\mu n}}\ \left(2.4\right).\]Ответ: По заданным в условии задачи параметрам среднеквадратичную скорость движения молекул газа вычислить можно с помощью формулы $\left\langle v_{kv}\right\rangle =\sqrt{\frac{3pN_A}{\mu n}}.$












