Закон (или распределение) Максвелла--Больцмана устанавливает распределение молекул газа по координатам и скоростям, если на систему действует внешнее потенциальное поле. Это распределение получают из так называемого распределения Гиббса(1):
где $W_p$- вероятность одного из состояний системы с энергией ${\varepsilon }_{p\ }$-- полная энергия, которой обладают частицы (кинетическая плюс потенциальная). Наиболее часто используют следующие формы распределения Максвелла-Больцмана.
Формы распределения Максвелла-Больцмана
Первая для концентрации частиц:
где $dn\left(v;x,y,z\right)$- число частиц, которые находятся в выделенном объеме газа $dV$, вблизи точки с координатами (x,y,z) и скорости этих молекул лежат в интервале от $v\ до\ v+dv;$ $v_{ver}$- наиболее вероятная скорость молекул, $m_0$- масса молекулы газа, $U\left(x,y,z\right)$- потенциальная энергия частицы в точке $\left(x,y,z\right)$; $n_0$- концентрация частиц газа в точке, которой потенциальную энергию приняли равной нулю.
Вторая для вероятности импульса и координаты:
где $dw\left(p_x,p_y,p_z,x,y,z\right)-\ \ $вероятность нахождения частицы в фазовом объеме $dxdydzdp_xdp_ydp_z$, около фазовой точки $\left(x,y,z,p_x,p_y,p_z\right)$, $U\left(x,y,z\right)$- потенциальная энергия молекулы во внешнем поле. В виде (3) распределение Максвелла-Больцмана можно рассматривать как произведение двух вероятностей независимых событий. Вероятности $dw\left(p_x,p_y,p_z\right)$того, что молекула обладает импульсом $\left(p_x,p_y,p_z\right)$ и вероятности $dw\left(x,y,z\right)$того, что она находится в точке $\left(x,y,z\right).$ Тогда уравнение (3) распадается на распределение Максвелла:
\[dw\left(p_x,p_y,p_z\right)=\frac{1}{{\left(2\pi m_0kT\right)}^{\frac{3}{2}}}{exp \left(-\frac{{p_x}^2+{p_y}^2+{p_z}^2}{2m_0kT}\right)\ }{dp}_xdp_ydp_z\ \left(4\right)\] \[dw\left(x,y,z\right)=Aex{p \left(-\frac{U\left(x,y,z\right)}{kT}\right)\ }dxdydz\ (5)\]Итак, распределения Максвелла и Больцмана являются составными частями распределения Гиббса. Энергия молекул, которые движутся в поле тяжести вверх, уменьшается, однако при распределении Максвелла по скоростям средняя энергия при этом постоянна. Сохранение средней энергии частиц, при уменьшении энергии отдельно взятой молекулы осуществляется благодаря выбыванию молекул с меньшей энергией из потока при увеличении высоты. Средняя энергия молекул, которые движутся вниз, не изменяется в результате присоединения к потоку молекул, которые выбыли из потока направленного вверх.
Сходство между распределениями Максвелла и Больцмана
Между распределениями Максвелла и Больцмана имеется существенное сходство: в обоих случаях эти законы содержат экспоненту, показатель которой в числителе содержит энергию молекулы (кинетическую у Максвелла, потенциальную у Больцмана) в знаменателе имеют величину --kT, которая определяет среднюю энергию теплового движения молекул. Это сходство в том числе, и позволяет объединить эти два распределения в один закон Максвела -- Больцмана.
Задание: Некоторый газ с неизменной массой переводят из одного равновесного состояния в другое. Изменяется ли в распределении молекул по скоростям: 1) положение максимума кривой в распределении Максвелла; 2) площадь под этой кривой?
Решение:
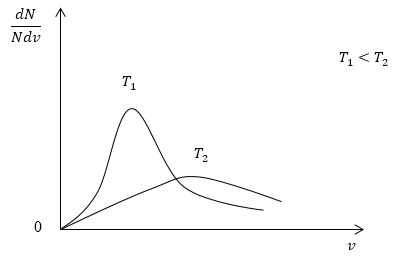
Рис. 1
Запишем распределение Максвелла молекул по модулю скорости:
\[\frac{dN}{Ndv}=4\pi {\left(\frac{m_0}{2\pi kT}\right)}^{\frac{3}{2}}exp\left(-\frac{m_0v^2}{2kT}\right)v^2\ (1.2)\]Если газ переводят из одного состояния равновесия в другое, следовательно, изменяется температура газа. Соответственно, положение максимума кривой Максвелла изменится.
Причем, если температура растет, максимум сдвигается в сторону больших скоростей, причем величина пика (высота по вертикальной оси) уменьшается (рис.1).
Площадь фигуры, которая ограничена кривой и осью скоростей на рис 1., равна 1 и не изменяется при изменении температуры.
Задание: Найти число молекул кислорода, скорости которых заключены в пределах от 195 м/c до 205 м/c при температуре T=273 K. Масса водорода (m) 0,1 кг.
Решение:
Интервал скоростей заданных в условии небольшой, можно использовать теорему о среднем, и тогда мы имеем:
\[\frac{\triangle N}{N}\approx 4\pi {\left(\frac{m_{O_2}}{2\pi kT}\right)}^{\frac{3}{2}}{exp \left(-\frac{m_{O_2}v^2}{2kT}\right)\ }v^2\triangle v\ \] \[\triangle N\approx 4\pi {N\left(\frac{m_{O_2}}{2\pi kT}\right)}^{\frac{3}{2}}{exp \left(-\frac{m_{O_2}v^2}{2kT}\right)\ }v^2\triangle v\ \left(2.1\right),\]где $v=$200 м/c, $\triangle v=10$ м/c, $\ \frac{m_{O_2}}{{\mu }_{O_2}}=\frac{1}{N_A}\to m_{O_2}=\frac{{\mu }_{O_2}}{N_A}$. $\frac{m}{{\mu }_{O_2}}=\frac{N}{N_A}\to N=\frac{mN_A}{{\mu }_{O_2}}$.
Подставим полученное в (2.1): $\triangle N\approx 4\pi {\frac{mN_A}{{\mu }_{O_2}}\left(\frac{\frac{{\mu }_{O_2}}{N_A}}{2\pi kT}\right)}^{\frac{3}{2}}{exp \left(-\frac{\frac{{\mu }_{O_2}}{N_A}v^2}{2kT}\right)\ }v^2\triangle v\ \left(2.2\right)$
Подставим в (2.2) численные значения, проведем расчет:
\[\triangle N\approx \approx \frac{4\cdot 3,14\cdot 0,1\cdot 6\cdot {10}^{23}}{32\cdot {10}^{-3}}{\left(\frac{\frac{32\cdot {10}^{-3}}{6\cdot {10}^{23}}}{2\cdot 3,14\cdot 1,38\cdot {10}^{-23}\cdot 273}\right)}^{\frac{3}{2}}{exp \left(-\frac{\frac{32\cdot {10}^{-3}}{6\cdot {10}^{23}}{\cdot \left(200\right)}^2}{2\cdot 1,38\cdot {10}^{-23}\cdot 273}\right)\ }{\cdot \left(200\right)}^2\cdot 10\approx 2,3\cdot {10}^{22}\]Ответ: Количество молекул кислорода при заданных условиях порядка $2,3\cdot {10}^{22}.$











