Переход вещества через критическое состояние характерен тем, что при этом исчезает различие между жидкой и газообразной фазами вещества. Критическое состояние характеризуется определенными для конкретного вещества параметрами: критическими температурой ($T_{kr})$, давлением ($p_{kr}$), объемом ($V_{kr}$). Если вещество, имеющее критическую температуру будет находиться в объеме не равном критическому, то состояние этого вещества критическим не будет. Различие между фазами в этом случае не исчезнет. Все вещество постепенно перейдет в одну фазу, при V${ > V}_{kr}$ вся жидкость испарится. При V${
Состояние реального газа
Рассмотрим реальный газ. Состояние такого газа опишем уравнением Ван-дер-Ваальса в виде:
Уравнение (1) является кубическим уравнением по отношению к объему, которое имеет переменные коэффициенты, зависящие от давления и температуры и свободный член. Такое уравнение может иметь Это уравнение имеет три корня. По отношению к решениям уравнения возможны следующие варианты в зависимости от соотношения коэффициентов: три вещественных корня, или один корень -- вещественный, два комплексных. Так как объем может быть только вещественным, то комплексные решения смысла не имеют. Начиная с температуры, которая называется критической, при любом давлении, вещественным является только один корень уравнения. Критическая температура каждая своя для вещества.
Изотерма для газа Ван-дер-Ваальса
Опыт показывает, что изотерма для газа Ван-дер-Ваальса имеет вид рис.1, то есть существуют области, в которых при изменении объема давление неизменно. В некоторых отрезках график изотермы параллелен оси V(рис 1). Это область фазового перехода, где жидкость и газ существую одновременно.
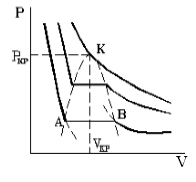
Рис. 1
По мере увеличения температуры участок отражающий состояние нахождения газа одновременно в двух фазах на графиках p(V) сужается, и превращается в точку (рис. 1). Это особая точка К, в которой пропадает различие между жидкостью и паром. Это так называемая критическая точка.
Касательная к критической точке К параллельна оси V. Следовательно, производная $\frac{dp}{dV}=0$ в точке К. Кроме того точка К является точкой перегиба, поэтому в ней равняется нулю и вторая производная: $\frac{d^2p}{dV^2}=0$.
Задание: Найдите критические параметры газа описываемого уравнением Ван-дер-Ваальса.
Решение:
В качестве основания для решения задачи запишем уравнение Ван-дер-Ваальса (для одного моля газа, соответственно в уравнении V=$V_{\mu }$):
\[\left(p+\frac{a}{V^2}\right)\left(V-b\right)=RT\left(1.1\right).\]Выразим из уравнения (1.1) давление, получим:
\[p=\frac{RT}{V-b}-\frac{a}{V^2}\ \left(1.2\right).\]Продифференцируем давление по объему ($\frac{dp}{dV})$:
\[\frac{dp}{dV}=-\frac{RT}{{\left(V-b\right)}^2}-\frac{2a}{V^3}\ \left(1.3\right).\]Найдем вторую производную:
\[\frac{d^2p}{dV^2}=\frac{2RT}{{\left(V-b\right)}^3}-\frac{6a}{V^4}\ \left(1.4\right).\]В критической точке первая и вторая производные раны нулю. Запишем:
\[\frac{dp}{dV}=-\frac{RT_{kr}}{{\left(V_{kr}-b\right)}^2}-\frac{2a}{{V_{kr}}^3}=0\ \left(1.5\right).\] \[\frac{d^2p}{dV^2}=\frac{2RT_{kr}}{{\left(V_{kr}-b\right)}^3}-\frac{6a}{{V_{kr}}^4}=0\ \left(1.6\right).\]И из (1.2) для критического давления имеем:
\[p_{kr}=\frac{RT_{kr}}{V_{kr}-b}-\frac{a}{{V_{kr}}^2}\ \left(1.7\right).\]Уравнения (1.5)-(1.7) образуют систему из трех уравнений с тремя неизвестными: $p_{kr},\ T_{kr},V_{kr}.$ Решая эту систему, получим:
\[V_{kr}=3b,\] \[p_{kr}=\frac{a}{27b^2},\] \[T_{kr}=\frac{8a}{27bR}.\]Так, зная постоянные Ван-дер-Ваальса a и b можно найти соответствующие критические параметры газа. И наоборот, по критическим параметрам газа можно вычислить константы уравнения Ван-дер-Ваальса.
Ответ: Критические параметры газа описываемого уравнением Ван-дер-Ваальса равны $V_{kr}=3b,p_{kr}=\frac{a}{27b^2},T_{kr}=\frac{8a}{27bR}.$
Задание: Какую часть объема сосуда должен занимать жидкий эфир при комнатной температуре, чтобы при достижении критической температуры он оказался в критическом состоянии? Для эфира $p_{kr}=35,5атм\ .,T_{kr}=467К,\ \ \ \mu =74\frac{г}{моль},\ \rho =714\frac{кг}{м^3}$
Решение:
Для решения задачи используем результаты, полученные в предыдущем примере, а именно:
\[V_{\mu kr}=3b,p_{kr}=\frac{a}{27b^2},T_{kr}=\frac{8a}{27bR}(2.1)\]Найдем из (2.1) $\frac{T_{kr}}{p_{kr}}$:
\[\frac{T_{kr}}{p_{kr}}=\frac{8a}{27bR}\frac{27b^2}{a}=\frac{8b}{R}\to b=\frac{T_{kr}}{p_{kr}}\frac{R}{8}\left(2.2\right)\] \[V_{\mu kr}=3b=\frac{{3T}_{kr}}{p_{kr}}\frac{R}{8}(2.3)\]Для того, чтобы наблюдался переход вещества через критическое состояние, необходимо, чтобы при достижении критической температуры занимаемый им объем был равен критическому объему. Плотность жидкой фазы:
\[\rho =\frac{m}{V_g}\left(2.4\right),\]где $V_g-\ $объем жидкости.
\[\frac{V_g}{V_{kr}}=\frac{V_g\mu }{mV_{\mu kr}}=\frac{\mu }{\rho V_{\mu kr}}\ \left(2.5\right),\]где $V_{\mu kr}$- критический молярный объем.
Используем (2.3) подставим $V_{\mu kr}$- в (2.5), получим:
\[\frac{V_g}{V_{kr}}=\frac{8\mu }{\rho R}\frac{p_{kr}}{{3T}_{kr}}\left(2.6\right).\]Прежде чем провести вычисления, переведём данные в СИ:
\[p_{kr}=35,5атм=35,5\cdot {10}^5Па,T_{kr}=467К,\ \ \ \mu =74\frac{г}{моль}=74\cdot {10}^{-3}\frac{кг}{моль}\]Подставим данные в (2.6), получим:
\[\frac{V_g}{V_{kr}}=\frac{8\cdot 74\cdot {10}^{-3}}{714\cdot 8,31}\frac{35,5\cdot {10}^5}{3\cdot 467}=0,25\ \left(2.7\right)\]Ответ: 0,25 часть объема сосуда должен занимать жидкий эфир.











