Что такое диффузия и коэффициент диффузии
Диффузией называется обусловленное тепловым движением выравнивание концентраций в смеси нескольких веществ.
Этот процесс наблюдается в газообразных, жидких и твердых средах. Пpи диффузии газов речь идет о проникновении одного газа в другой за счет теплового движения. Пpи диффузии переносится масса некоторого компонента в смеси газов. Опыт показывает, что плотность потока диффузии (число диффундирующих молекул в секунду через единичную площадку, ориентированную перпендикулярно потоку диффузии) пропорциональна градиенту молекулярной плотности данного компонента смеси. То есть:
\[j_d=-D\frac{dn}{dx}\left(1\right),\]где D -- коэффициент диффузии. Плотность потока концентрации частиц пропорциональна производной $\frac{dn}{dx}$ -- проекции градиента концентрации на ось Ox (часто эту производную называют градиентом -- это не совсем правильно, так как градиент векторная величина).
Вследствие теплового движения возникает поток молекул каждой компоненты в направлении убывания ее концентрации. Экспериментально установлено, что поток молекул i- ой компоненты через перпендикулярную к оси Ox поверхность S определяется уравнением:
\[N_i==-D\frac{dn_i}{dx}S\left(2\right).\]Знак минус обусловлен тем, что поток направлен в сторону убывания концентрации. Умножив (2) на массу молекулы i-й компоненты $m_i$, получим уравнение диффузии для потока массы i-й компоненты:
\[M_i=-D\frac{d{\rho }_i}{dx}S\left(3\right),\]где ${\rho }_i=n_im_i$ -- парциальная плотность i - компоненты (ее можно называть абсолютной концентрацией). Явление диффузии в одномерном случае в двухкомпонентной системе называется первым законом Фика (3). Уравнение (3) получено эмпирическим путем.
Получим коэффициент диффузии, исходя из представлений МКТ о явлениях переноса в газах. Рассмотрим двухкомпонентную смесь. Будем предполагать, что молекулы газа движутся только в трех взаимно перпендикулярных направлениях. Отступая от единичной площадки М на длину свободного пробега вправо и влево, построим куб единичного объема. В среднем одна шестая часть молекул этих кубиков летит по направлению к площадке. В соответствии с этим количество молекул, пролетающих через единичную воображаемую площадку в единицу времени:
\[\nu =\frac{1}{6}n\left\langle v\right\rangle \ \left(4\right),\]где $\left\langle v\right\rangle \ $- средняя скорость молекул.
При небольших нарушениях процессов равновесия считаем, что:
\[\frac{dn}{d\lambda }\lambda \ll n,\ \]где $\lambda $ -- длина свободного пробега молекулы. Молекулы обеих компонент мало отличаются по массе $m_1\approx m_2\approx m$, имеют одинаковые эффективные сечения $\sigma_1\approx \sigma_2\approx \sigma$. При этих условиях молекулы обеих компонент имеют одинаковые средние скорости $\left\langle v\right\rangle $, а длину свободного пробега можно вычислять по формуле:
\[\lambda =\frac{1}{\sqrt{2}\sigma n},\ n=n_1+n_2\left(5\right).\]Чем реже сталкиваются молекулы, и чем выше их скорость, тем диффузия проходит интенсивнее, поэтому запишем:
\[D\sim \left\langle v\right\rangle \lambda \left(6\right).\]Обозначим число молекул первой компоненты, пролетающих в единицу времени сквозь воображаемую поверхность S в направлении оси Ox, через $N'_1$, для противоположного направления $N^{''}_1$. $N'_1-N^{''}_1$=$N_1$ -- поток частиц первого вещества через поверхность S. Используем (4), получим:
\[N'_1=\frac{1}{6}n'_1\left\langle v\right\rangle S,N'_2=\frac{1}{6}n'_2\left\langle v\right\rangle S\ \left(7\right),\]$n'_1$- «эффективная концентрация» первой компоненты слева от S, $n'_2$- «эффективная концентрация» первой компоненты справа от S. Через поверхность S пролетают молекулы, которые свое последнее соударение претерпели на расстоянии $л$ от нее (в среднем). Поэтому:
\[n'_1=n_1\left(x-л\right),\ n'_2=n_2\left(x+\lambda \right)\left(8\right).\]Используем формулу (7):
\[N_1=\frac{1}{6}\left\langle v\right\rangle S{\left[n_1\left(x-\lambda \right)-n_1\left(x+\lambda \right)\right]\left(9\right).}\]Так как $\lambda $- очень мала, $n_1\left(x- \lambda \right)-n_1\left(x+\lambda \right)=-\frac{dn_1}{dx}2\lambda \left(10\right).$
Подставим (10) в (9):
\[N_1=-\left(\frac{1}{3}\left\langle v\right\rangle \lambda \right)\frac{dn_1}{dx}S\left(11\right).\]Так, мы получили уравнение диффузии для первой компоненты, кроме того, сравнив (11) с (2), получим:
\[D=\frac{1}{3}\left\langle v\right\rangle \lambda \ \left(12\right).\]Так как мы предположили, что массы молекул обеих компонент по массе и эффективному сечению равны, то, вообще говоря, мы имеем дело с самодиффузией (диффузией молекул газа между молекулами того же газа).
Задание: В вакууме находится сосуд объемом V заполненный воздухом, температура которого постоянна, в некоторый момент времени (t=0) в сосуде образовалось очень маленькое отверстие, и газ стал вытекать. $N_0$-начальное число молекул, $\left\langle v\right\rangle $ -- средняя скорость молекул. Найти закон изменения числа молекул в сосуде N(t).

рис. 1
Решение:
Запишем уравнение плотности потока концентрации:
\[j_d=-D\frac{dn}{dx}\left(1.1\right),\]где
\[D=\frac{1}{6}\left\langle \lambda \right\rangle \left\langle v\right\rangle \to j_d=-\frac{1}{6}\left\langle \lambda \right\rangle \left\langle v\right\rangle \frac{n}{\left\langle \lambda \right\rangle }S=\frac{1}{6}n\left\langle v\right\rangle S\left(1.2\right)\] \[dN=jdt=-\frac{1}{6}n\left\langle v\right\rangle Sdt=-\frac{1}{6}\frac{N}{V}S\left\langle v\right\rangle dt\left(1.3\right)\] \[\frac{dN}{N}=-\frac{1}{6}\frac{S}{V}\left\langle v\right\rangle dt\left(1.4\right)\] \[lnN=-\frac{1}{6}\frac{\left\langle v\right\rangle }{V}St+lnC\left(1.5\right)\] \[N=Ce^{-\frac{1}{6}\frac{\left\langle v\right\rangle }{V}St}\left(1.6\right)\]По условиям задачи при t=0 начальное число молекул $N_0$, следовательно:
\[N_0=С,\ N=N_0e^{-\frac{1}{6}\frac{\left\langle v\right\rangle }{V}St}\]Изобразим график закона изменения числа молекул в сосуде.
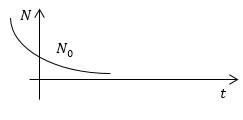
рис. 2
Ответ: Закон изменения числа молекул в сосуде N(t)=$\ Ce^{-\frac{1}{6}\frac{\left\langle v\right\rangle }{V}St}$ изображен на рис.1.
Задание: Найдите коэффициент диффузии D воздуха при давлении p и температуре T. Диаметр молекулы воздуха d.
Решение:
Запишем выражение для коэффициента диффузии:
\[D=\frac{1}{3}\left\langle v\right\rangle \lambda \left(2.1\right),\]где
\[\left\langle v\right\rangle =\sqrt{\frac{8RT}{\pi \mu }}\left(2.2\right)\]Длина свободного пробега молекулы (($\sigma=\pi d^2$), $\sigma$ -- эффективное сечение молекулы):
\[л=\frac{1}{\sqrt{2}\sigma n}=\frac{1}{\sqrt{2}\pi d^2n}\left(2.3\right)\]Из основного уравнения МКТ (p=nkT), имеем:
\[n=\frac{p}{kT}\to \lambda=\frac{kT}{\sqrt{2} \pi d^2p}\left(2.4\right)\]Используем (2.2) и (2.5), подставим в (2.1), получим:
\[D=\frac{1}{3}\sqrt{\frac{8RT}{\pi \mu}}\frac{kT}{\sqrt{2} \pi d^2p}\]Ответ: Коэффициент диффузии воздуха D$=\frac{1}{3}\sqrt{\frac{8RT}{\pi \mu}}\frac{kT}{\sqrt{2}\pi d^2p}.$











