Работа выхода
Факт существования твердых тел говорит о том, что существуют силы, которые удерживают, находящиеся в постоянном движении электроны внутри тела. Для того чтобы из тела извлечь электрон, следует затратить работу. Допустим, что твердое тело находится внутри адиабатической оболочки при постоянной температуре T. В результате теплового движения и перераспределения электронов по скоростям внутри тела кинетической энергии некоторых электронов будет достаточно для преодоления сил, которые удерживают их внутри тела. Из-за этого у поверхности тела возникает «газ» из электронов. Некоторые электроны приближаются к поверхности тела и захватываются внутрь тела. В состоянии термодинамического равновесия среднее количество электронов, покидающих тело, равно среднему числу электронов возвращающихся. Этот «электронный газ» не вырожден, его плотность может быть записана в виде распределения Больцмана:
где $n_0$ -- концентрация электронов у поверхности тела, C -- зависит только от температуры, $A_Ф$ --работа выхода. Работа выхода связана с энергией $\mu $ уровня Ферми соотношением:
где $E_0$ -- энергия покоящегося электрона вне проводника в вакууме. То есть $A_Ф$ равна работе по перемещению электрона с уровня $\mu $ за пределы твердого тела. Для металлов это утверждение буквально, для диэлектриков несколько условно, так как в них на уровне Ферми нет электронов.
Силы, которые удерживают электроны в твёрдых телах, имеют электрическое происхождение. Они вызваны разностью потенциалов между точками вне тела и внутренними точками. Силы, которые стремятся втянуть электроны внутрь тела тем больше, чем больше работа выхода $A_Ф.$ Они действуют в очень тонком слое (порядка молекулярных размеров $d\approx {10}^{-10}м$). Эффективная напряженность электрического поля ($E_{ef}$), которое вызывает появление этих сил порядка:
где работа выхода принята равной нескольким электрон- вольтам. Работу выхода электронов из металла часто выражают в электрон -- вольтах. Это внесистемная единица $1эB=1,602\cdot {10}^{-19}Дж.$
Контактные явления
Если сблизить поверхности двух тел так близко, что слои их электронного газа перекроются, то тела станут обмениваться электронами. Силы, которые увлекают электрон в тело будут больше у того тела у которого работа выхода больше. После того как сблизили тела с их поверхностей начнется переход электронов от вещества с меньшей работой выхода к веществу с большей работой. Как результат первое тело будет заряжаться положительно, второе отрицательно. Возникающее между телами электрическое поле будет препятствовать движению электронов в результате которого, оно появилось. В состоянии равновесия напряженность поля достигает такого значения, что переход электронов прекращается. Поверхности имеют одинаковые по величине, но противоположные по знаку заряды. Между поверхностями устанавливается некоторая разность потенциалов, которая называется контактной.
Появление контактной разности потенциалов было открыто Вольтой в 1797 г. у металлов. Он расположил металлы в ряд, заметил, что если металлы в определенной им последовательности привести в контакт, то при этом каждый предыдущий металл получит более высокий потенциал, чем следующий. Причем, если несколько металлов одинаковой температуры, привести в контакт, то разность потенциалов между крайними металлами не зависит от того, какими промежуточными металлами они разделяются (закон последовательных контактов Вольты). Если крайние металлы замкнуть в кольцо, то ЭДС в кольце будет равна нулю. Иначе был бы нарушен закон сохранения энергии. Данное положение не применяется, если в цепи есть электролиты, и могут течь химические реакции.
Контактная разность потенциалов
Для того чтобы объяснить существование контактной разности потенциалов можно использовать модель свободных электронов. Если T=0K, то все уровни энергии до границы Ферми ($\mu $) будет заполнены электронами.
где $n\ $-- концентрация электронов проводимости.
Допустим, что мы привели в контакт два металла (1) и (2) с энергиями Ферми равными соответственно ${\mu }_1\ \[{\mu }_1+q_e{\varphi }_{i1}=м_2+q_eц_{i2}\left(4\right).\]
Следовательно,
Так как $q_e{\varphi }_{i1}$.
Этот результат справедлив и при $T\ne 0.$ В формуле (5) считают, что точка 1 лежит внутри металла (1), а точка 2 внутри второго металла. Это отмечено индексом $i$. Разность потенциалов ${\varphi }_{i2}-{\varphi }_{i1}$ называют внутренней контактной разностью потенциалов. Из формулы (5) следует, что внутренняя контактная разность потенциалов удовлетворяет закону последовательных контактов Вольты. Используя формулу (3), получим:
Допустим, что между металлами есть зазор микроскопической величины. Возьмем внутри зазора точки $1'\ и\ 2'$, которые лежат на расстоянии порядка чуть больше, чем толщина поверхностного слоя от границ соответствующих металлов. Потенциалы во внешних точках обозначим как ${\varphi }_{e2}\ и\ {\varphi }_{e1}$. Их разность называют внешней контактной разностью потенциалов. Величину внешней контактной разности потенциалов определяют как:
где $A_2,A_1$ -- работы выхода на границах металлов. Присутствие внешней контактной разности потенциалов означает, что в зазоре между металлами есть электрическое поле.
Внешняя контактная разность потенциалов также подчиняется закону контактов Вольты.
Задание: Оцените, чему равна внутренняя контактная разность потенциалов для меди.
Решение:
В качестве основы для решения задачи используем формулу:
\[{\varphi }_{i2}-{\varphi }_{i1}=\frac{h^2}{8m_eq_e}{\left(\frac{3}{\pi }\right)}^{\frac{2}{3}}\left({n_1}^{\frac{2}{3}}-{n_2}^{\frac{2}{3}}\right)\left(1.1\right),\]где $h=6,63\cdot {10}^{-34}Дж\cdot с,$ $m_e=9,1\ \cdot {10}^{-31}кг$, $q_e=1,6\cdot {10}^{-19}Кл.$ Если на каждый атом приходится один свободный электрон, тогда, получим:
\[{\varphi }_{i2}-{\varphi }_{i1}=-3,66\cdot {10}^{-15}n^{\frac{2}{3}}\sim 1\ \left(B\right).\]Ответ: Для меди ${\varphi }_{i2}-{\varphi }_{i1}\approx 1\ В.$
Задание: Схематично изобразите образование контактной разности потенциалов между двумя металлами и между двумя диэлектриками.
Решение:
Отличие в образовании контактной разности потенциалов в металлах и диэлектриках состоит том, что электрическое поле не проникает внутрь металлов, но проникает на небольшую глубину внутрь диэлектриков ($d_2-глубина\ проникновения\ поля\ в\ диэлектрике$). У диэлектрика падение потенциала происходит не только между поверхностями, но и частично в тонком слое внутри диэлектрика около его поверхности. Но, надо сказать, что толщина этого слоя мала в сравнении с расстоянием между поверхностями, поэтому часто им пренебрегают.
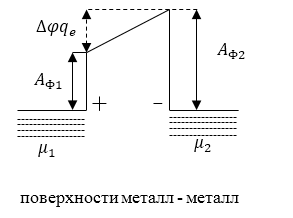
Рисунок 1.
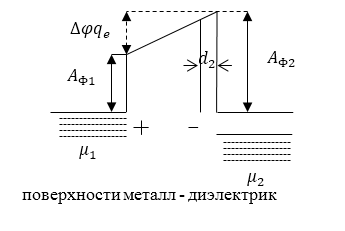
Рисунок 2.
Из рис. 1 видно, что разность между энергий верхних точек потенциальных ям равна $A_{Ф2}-A_{Ф1}$. Значит контактная разность потенциалов между поверхностями тел, в случае их равновесия, задана формулой:
\[\triangle \varphi =\frac{\left|A_{Ф2}-A_{Ф1}\right|}{\left|q_e\right|}\ \left(2.1\right).\]











