
Определение магнитной проницаемости вещества. Ее роль в описании магнитного поля
Если провести опыт с соленоидом, который соединен с баллистическим гальванометром, то при включении тока в соленоиде можно определять значение магнитного потока Ф, который будет пропорционален отбросу стрелки гальванометра. Проведем опыт дважды, причем ток (I) в гальванометре установим одинаковый, но в первом опыте соленоид будет без сердечника, а во втором опыте, перед тем как включить ток, введем в соленоид железный сердечник. Обнаруживается, то, что во втором опыте магнитный поток существенно больше, чем в первом (без сердечника). При повторении опыта с сердечниками разной толщины, получается, максимальный поток получается в том случае, когда весь соленоид заполнен железом, то есть обмотка плотно навита на железный сердечник. Можно провести опыт с разными сердечниками. В результате получается, что:
где $Ф$ -- магнитный поток в катушке с сердечником, $Ф_0$ -- магнитный поток в катушке без сердечника. Увеличение магнитного потока при введении в соленоид сердечника объясняется тем, что к магнитному потоку, который создает ток в обмотке соленоида, добавился магнитный поток, создаваемый совокупностью ориентированных амперовых молекулярных токов. Под влиянием магнитного поля молекулярные токи ориентируются, и их суммарный магнитный момент перестает быть равным нулю, возникает дополнительное магнитное поле.
Величину $\mu $, которая характеризует магнитные свойства среды, называют магнитной проницаемостью (или относительной магнитной проницаемостью).
Это безразмерная характеристика вещества. Увеличение потока Ф в $\mu $ раз (1) означает, что магнитная индукция $\overrightarrow{B}$ в сердечнике во столько же раз больше, чем в вакууме при том же токе в соленоиде. Следовательно, можно записать, что:
\[\overrightarrow{B}=\mu {\overrightarrow{B}}_0\left(2\right),\]где ${\overrightarrow{B}}_0$ -- магнитная индукция поля в вакууме.
Наряду с магнитной индукцией, которая является основной силовой характеристикой поля, используют такую вспомогательную векторную величину как напряженность магнитного поля ($\overrightarrow{H}$), которая связана с $\overrightarrow{B}$ следующим соотношением:
\[\overrightarrow{B}=\mu \overrightarrow{H}\left(3\right).\]Если формулу (3) применить к опыту с сердечником, то получим, что в отсутствии сердечника:
\[{\overrightarrow{B}}_0={\mu }_0\overrightarrow{H_0}\left(4\right),\]где $\mu $=1. При наличии сердечника мы получаем:
\[\overrightarrow{B}=\mu {\mu }_0\overrightarrow{H}\left(5\right).\]Но так как выполняется (2), то получается, что:
\[\mu {\mu }_0\overrightarrow{H}={\mu м}_0\overrightarrow{H_0}\to \overrightarrow{H}=\overrightarrow{H_0}\left(6\right).\]Мы получили, что напряженность магнитного поля не зависит от того, каким однородным веществом заполнено пространство. Магнитная проницаемость большинства веществ около единицы, исключения составляют ферромагниетики.
Магнитная восприимчивость вещества
Обычно вектор намагниченности ($\overrightarrow{J}$) связывают с вектором напряженности в каждой точке магнетика:
\[\overrightarrow{J}=\varkappa \overrightarrow{H}\left(7\right),\]где $\varkappa $ -- магнитная восприимчивость, безразмерная величина. Для неферромагнитных веществ и в не больших полях $\varkappa $ не зависит от напряженности, является скалярной величиной. В анизотропных средах $\varkappa $ является тензором и направления $\overrightarrow{J}$ и $\overrightarrow{H}$ не совпадают.
Связь между магнитной восприимчивостью и магнитной проницаемостью
По определению вектора напряжённости магнитного поля:
\[\overrightarrow{H}=\frac{\overrightarrow{B}}{{\mu }_0}-\overrightarrow{J}\left(8\right).\]Подставим в (8) выражение для вектора намагниченности (7), получим:
\[\overrightarrow{H}=\frac{\overrightarrow{B}}{{\mu }_0}-\overrightarrow{H}\left(9\right).\]Выразим напряженность, получим:
\[\overrightarrow{H}=\frac{\overrightarrow{B}}{{\mu }_0\left(1+\varkappa \right)}\to \overrightarrow{B}={\mu }_0\left(1+\varkappa \right)\overrightarrow{H}\left(10\right).\]Сравнивая выражения (5) и (10), получим:
\[\mu =1+\varkappa \left(11\right).\]Магнитная восприимчивость может быть как положительной так и отрицательной. Из (11) следует, что магнитная проницаемость может быть как больше единицы, так и меньше нее.
Задание: Вычислите намагниченность в центре кругового витка радиуса R=0,1 м с током силой I=2A, если он погружен в жидкий кислород. Магнитная восприимчивость жидкого кислорода равна $\varkappa =3,4\cdot {10}^{-3}.$
Решение:
За основу решения задачи примем выражение, которое отражает связь напряженности магнитного поля и намагниченности:
\[\overrightarrow{J}=\varkappa \overrightarrow{H}\left(1.1\right).\]Найдем поле в центре витка с током, так как намагниченность нам необходимо вычислит в этой точке.
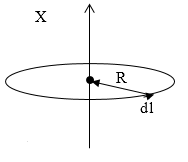
Рис. 1
Выберем на проводнике с током элементарный участок (рис.1), в качестве основы для решения задачи используем формулу напряженности элемента витка с током:
\[dH=\frac{1}{4\pi }\frac{Idlsin \vartheta}{r^2}\left(1.2\right),\]где$\ \overrightarrow{r}$- радиус-вектор, проведенный из элемента тока в рассматриваемую точку, $\overrightarrow{dl}$- элемент проводника с током (направление задано направлением тока), $\vartheta$ -- угол между $\overrightarrow{dl}$ и $\overrightarrow{r}$. Исходя из рис. 1 $\vartheta=90{}^\circ $, следовательно (1.1) упростится, кроме того расстояние от центра окружности (точки, где мы ищем магнитное поле) элемента проводника с током постоянно и равно радиусу витка (R), следовательно имеем:
\[dH=\frac{1}{4\pi }\frac{Idl}{R^2}\left(1.3\right).\]Результирующий вектор напряженности магнитного поля направлен по оси X, его можно найти как сумму отдельных векторов$\ \ \overrightarrow{dH},$ так как все элементы тока создают в центре вика магнитные поля, направленные вдоль нормали витка. Тогда по принципу суперпозиции полную напряженность магнитного поля можно получить, если перейти к интегралу:
\[H=\oint{dH\ \left(1.4\right).}\]Подставим (1.3) в (1.4), получим:
\[H=\frac{1}{4\pi }\frac{I}{R^2}\oint{dl}=\frac{1}{4\pi }\frac{I}{R^2}2\pi R=\frac{1}{2}\frac{I}{R}(1.5).\]Найдем намагниченность, если подставим напряженность из (1.5) в (1.1), получим:
\[J=\frac{\varkappa }{2}\frac{I}{R}\ \left(1.6\right).\]Все единицы даны в системе СИ, проведем вычисления:
\[J=\frac{3,4\cdot {10}^{-3}}{2}\cdot \frac{2}{0,1}=3,4\cdot {10}^{-2}\left(\frac{А}{м}\right).\]Ответ: $J=3,4\cdot {10}^{-2}\frac{А}{м}.$
Задание: Вычислите долю суммарного магнитного поля в вольфрамовом стержне, который находится во внешнем однородном магнитном поле, которую определяют молекулярные токи. Магнитная проницаемость вольфрама равна $\mu =1,0176.$
Решение:
Индукцию магнитного поля ($B'$), которая приходится на долю молекулярных токов, можно найти как:
\[B'={\mu }_0J\ \left(2.1\right),\]где $J$ -- намагниченность. Она связана с напряженностью магнитного поля выражением:
\[J=\varkappa H\ \left(2.2\right),\]где магнитную восприимчивость вещества можно найти как:
\[\varkappa =\mu -1\ \left(2.3\right).\]Следовательно, магнитное поле молекулярных токов найдем как:
\[B'={\mu }_0\left(\mu -1\right)H\left(2.4\right).\]Полное поле в стержне вычисляется в соответствии с формулой:
\[B=\mu {\mu }_0H\ \left(2.5\right).\]Используем выражения (2.4) и (2.5) найдем искомое соотношение:
\[\frac{B'}{B}=\frac{{\mu }_0\left(\mu -1\right)H}{\mu {\mu }_0H}=\frac{\mu -1}{\mu }.\]Проведем вычисления:
\[\frac{B'}{B}=\frac{1,0176-1}{1,0176}=0,0173.\]Ответ:$\frac{B'}{B}=0,0173.$











