При переходе границы между двумя магнетиками с разными магнитными проницаемостями $(\mu )$ векторы напряжённости ($\overrightarrow{H}$) и индукции ($\overrightarrow{B}$) испытывают скачкообразные изменения, которые описываются граничными условиями.
Касательная составляющая вектора напряженности магнитного поля
Получим граничное условие для тангенциальной составляющей вектора $\overrightarrow{H}$магнитного поля ($H_{\tau }$). Предположим, что вдоль границы раздела течет поверхностный ток проводимости линейной плотности $\overrightarrow{j}$. Построим около границы магнетиков 1 и 2 замкнутый контур (рис. 1).
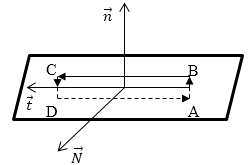
Рис. 1
Согласно теореме о циркуляции запишем, что:
У этого контура высота пренебрежимо мала по сравнению с длинной основания $l$. Следовательно, вкладом в циркуляцию магнитного поля боковых сторон (AB и СD) пренебрежем. В таком случае имеем:
Правая часть выражения (1) имеет вид:
где $j_n$ --составляющая поверхностной плотности тока вдоль нормали к контуру $\overrightarrow{N}=\left[\overrightarrow{n}\overrightarrow{t}\right]\ $(или, говорят в направлении перпендикулярном тому, в котором выбирают касательные составляющие $\overrightarrow{H}$). Надо отметить, что это поверхностные токи проводимости, а не молекулярные токи. Приравняем правые части выражений (2) и (3), получим:
В векторном виде имеем:
В том случае, если тока проводимости на границе раздела нет, то касательные составляющие $\overrightarrow{H\ }$на границе раздела непрерывны:
Нормальная составляющая вектора магнитной индукции поля
Граничное условие для $B_n$получают из уравнения:
Перпендикулярные составляющие $\overrightarrow{B}$на границе раздела двух магнетиков непрерывны:
Нормальная составляющая вектора $\overrightarrow{H}$Из уравнения (8), если применить материальное уравнение для векторов магнитного поля при переходе из одной среды в другую имеем:
Касательная составляющая вектора $\overrightarrow{B}$ магнитного поля
Тангенциальные составляющие магнитного поля испытываю скачек, причем:
Выражения (4, 6), (8), (9), (10) являются граничными условиями для магнитного поля. Они аналогичны граничным условиям для электрического поля.
Закон преломления линий магнитного поля
Из граничных условий для магнитного поля следует закон преломления линий индукции:
где ${\alpha }_1$ -- угол между линиями магнитной индукции в среде 1 и нормалью к поверхности раздела, ${\alpha }_2$- гол в среде 2. Так как в изотропных средах направления вектора $\overrightarrow{B}$ и вектора $\overrightarrow{H}$ совпадают, то закон (11) является и законом преломления линий напряженности. Из (11) следует, что если линии поля переходят из среды с меньшей магнитной проницаемостью в среду с большей проницаемостью, то они удаляются от нормали, и линии сгущаются.
Задание: На рис. 2 изображены линий вектора $\overrightarrow{B}\ $при переходе их одного магнетика (${\mu }_1$) в другой (${\mu }_2$). Какая из магнитных проницаемостей среды больше?
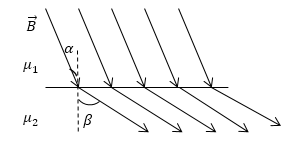
Рис. 2
Решение:
Рассмотрим, поведение силовых линий, когда они переходят границу двух магнетиков. Если отсутствуют поверхностные токи, выполняется условие:
\[\frac{tg\alpha }{tg\beta }=\frac{B_{1\tau }}{B_{2\tau }}=\frac{{\mu }_1}{{\mu }_2}\ \left(1.1\right).\]Это означает, что в магнетике с большей магнитной проницаемостью, вектор $\overrightarrow{B}$ составляет больший угол с нормалью к границе раздела двух магнетиков.
Следовательно, в нашей задаче ${\mu }_2 > {\mu }_1$.
Ответ: ${\mu }_2 > {\mu }_1$.
Задание: Магнитное поле на границе двух магнетиков изобразили с помощью линий поля (рис.3). Какие это линии, какая из магнитных проницаемостей среды больше?
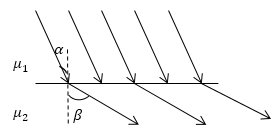
Рис. 3
Решение:
- На рис.3 изображены линии напряженности магнитного поля ($\overrightarrow{H}$), так как мы знаем, что они на границе магнетиков испытывают разрыв. Это является следствием связанных токов на границе раздела. Тогда как линии индукции магнитного поля не прерываются.
- ${\mu }_2 > {\mu }_1,$ так как в среде с большей магнитной проницаемостью линии поля имею больший угол между нормалью к границе раздела сред согласно закону преломления.
Ответ: 1. Линии напряженности магнитного поля. 2. ${\mu }_2 > {\mu }_1$.
Задание: В однородное поле помещают шар из магнетика, изобразите линии индукции магнитного поля. Считайте, что магнитная проницаемость шара больше, чем проницаемость окружающей среды.
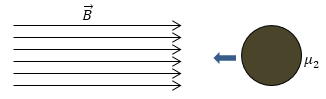
Рис. 4
Решение:
В ситуации, которая задана линии индукции в теле шаровой формы будут параллельными линиями, значение индукции во всех точках шара одинаковое. При этом будут постоянны напряженность и намагниченность, то есть, говорят, что шар намагничен однородно. Кроме того рис. 5 учитывает, что ${\mu }_2 > {\mu }_1.$
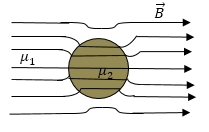
Рис. 5











