Гистерезис
Ферромагнетики обнаруживают свойство, которое по форме аналогично свойству сегнетоэлектриков, а именно гистерезис. Магнитная индукция (или намагниченность) ферромагнетиков не только не линейна относительно напряженности магнитного поля, но и зависит от истории намагничивания.
Допустим, что мы намагничиваем первоначально не намагниченный ферромагнетик, помещая его внутрь намагничивающей катушки. Увеличим напряжённость поля от нуля, до $H_{1\ }$(рис.1). Зависимость B(H) определена отрезком О1 кривой О1А и при напряженности поля равной $H_{1\ }$ индукция магнитного поля равна $B_{1\ }$. Если теперь уменьшать напряженность магнитного поля, то изменение магнитной индукции будет изображено не отрезком О1.
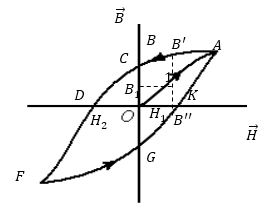
Рис. 1
Участок OA на рис. 1 называют основной кривой намагничивания, так как включение поля проводят при B=0, постоянной намагниченности нет. Замкнутая кривая ACDFGKSA -- петля гистерезиса. Если уменьшать напряжённость магнитного поля от точки А до нуля, то индукция магнитного поля ферромагнетика уменьшится до индукции в точке C. Такая индукция называется остаточной. В этом состоянии ферромагнетик -- постоянный магнит.
Для ликвидации остатков магнитного поля следует приложить обратное поле, напряженность которого равна $H_2$. Такая напряженность называется коэрцитивной силой ферромагнетика.
Аналогично рис.1 получается петля на диаграмме намагниченности J(H). Если при этом максимальное значение напряженности поля таково, что намагниченность достигает насыщения, то получают максимальную петлю гистерезиса. Если такового напряжения поля не достигает, то петлю гистерезиса называют частным циклом. Частных циклов может существовать бесконечно много, и все они лежат внутри максимальной петли.
Гистерезис приводит к тому, что индукция магнитного поля не является однозначной функцией от напряженности. Она существенно зависит от истории намагничивания. Так, в поле с напряженностью $H_1$ индукция может иметь значение в интервале от $B'_1до\ B^{''}_1\ $(рис.1).
Форма петли гистерезиса, остаточная индукция, коэрцитивная сила зависит от вещества ферромагнетика и может существенно изменяться.
Кривая Столетова
Характерной особенностью ферромагнетиков является сложная нелинейная зависимость между намагниченностью ($\overrightarrow{J}$) и напряженностью магнитного поля ($\overrightarrow{H}$) или индукцией магнитного поля ($\overrightarrow{B}$) и напряженностью. Первым подробные исследования для железа были проведены А.Г. Столетовым.
Мы помним, что напряженность магнитного поля и его индукция связаны соотношением:
Для ферромагнетиков магнитная проницаемость ($\mu $) -- не является постоянной и зависит от напряженности магнитного поля, вообще в связи с неоднозначностью связи B(H) само понятие магнитной проницаемости применяют только к основной кривой намагничивания. Изобразим на рис.2 (a) основную кривую намагничивания. Проведем из начала координат прямую через любую точку кривой. Тангенс угла наклона этой прямой пропорционален отношению $\frac{B}{H}$, то есть пропорционален магнитной проницаемости для соответствующего значения напряженности. При росте напряженности от нуля до некоторого значения $\mu $ сначала растет, в точке 2 достигает максимума, затем падает. Максимальное значение магнитной проницаемости достигает максимума раньше, чем наступает насыщение.
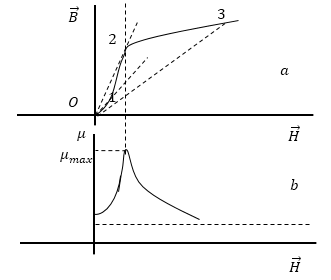
Рис. 2
При бесконечном увеличении напряженности внешнего поля $\mu $ асимптотический стремится к единице. Это является следствием того, что намагниченность не может превысить $J_{max}$, в выражении:
Кривая, изображенная на рис 2 (б), называется кривой Столетова.
Задание: Как полностью размагнитить ферромагнетик, если он имеет намагниченность отличную от нуля.
Решение:
Для того чтобы размагнитит ферромагнетик его можно поместить в переменное магнитное поле, которое создается, например, катушкой с током. Силу тока уменьшим до нуля. При этом в магнитном поле катушки ферромагнетик подвергается многократным циклическим перемагничиваниям, которые соответствуют разным петлям гистерезиса, которые постепенно уменьшаются и стягиваются к точке O (рис.1), где намагниченность равна нулю.
Задание: Укажите, в каком из циклов ACDF или KLMN один и тот же ферромагнетик нагреется больше.
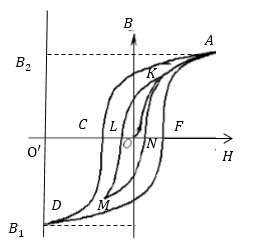
Рис. 3
Решение:
Рассмотрим цикл ACDF. Чтобы значение индукции увеличить от $B_1$ до $B_2$, требуется работа равная площади, которая ограничена ветвью кривой намагничивания DFA или площади фигуры $B_1DFAB_2$, при размагничивании до исходного состояния возвращаемая работа равна площади фигуры $B_2ACDB_1\ $(которая, очевидно меньше). При полном цикле перемагничивания в каждую единицу объема магнетика вводится энергия w равная:
\[w=S\ \left(2.1\right),\]где S -- площадь петли гистерезиса. Эта работа расходуется на преодоление коэрцитивных сил в магнетике и в конечном итоге превращается в тепло. Поэтому ферромагнетики при циклическом перемагничивании нагреваются. Чем больше площадь петли гистерезиса, тем больше нагрев.
Ответ: В цикле ACDF ферромагнетик нагреется больше.











