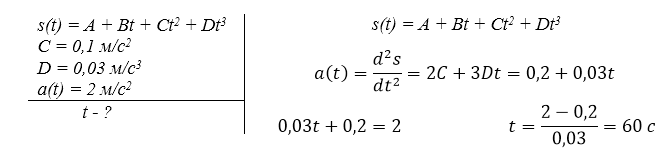В зависимости от формы траектории, движение делится на прямолинейное и криволинейное. В реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца движение планет, конца стрелки часов по циферблату и т.д.
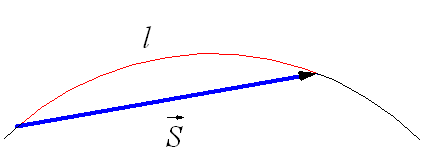
Рисунок 1. Траектория и перемещение при криволинейном движении
Криволинейное движение -- это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). При движении по криволинейной траектории вектор перемещения $\overrightarrow{s}$ направлен по хорде (рис. 1), а l -- длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 2).
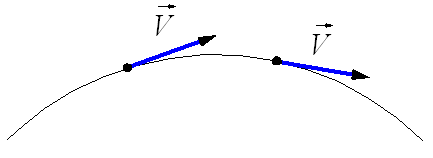
Рисунок 2. Мгновенная скорость при криволинейном движении
Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).
Криволинейное движение -- это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.
Для исследования криволинейного движения материальной точки применимы два разных подхода.
Можно разбить движение на отдельные участки, на каждом из которых движение можно считать прямолинейным (рис. 3).
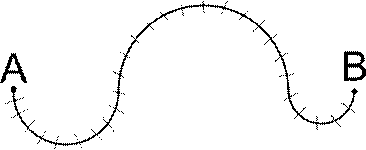
Рисунок 3. Разбиение криволинейного движения на поступательные движения
А дальше на каждом из этих участков мы можем пользоваться законами прямолинейного движения, которые мы уже знаем. В принципе, такой подход возможен.
Однако более удобным является следующий подход. Можно представить это движение как совокупность нескольких движений по дугам окружностей (см. рис. 4.). Таких разбиений получится меньше, чем в предыдущем случае, кроме того, движение по окружности само является криволинейным.
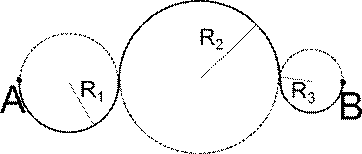
Рисунок 4. Разбиение криволинейного движения на движения по дугам окружностей
Для того, чтобы описывать криволинейное движение, нужно научиться описывать движение по окружности, а потом произвольное движение представлять в виде совокупностей движений по дугам окружностей.
Задачей исследования криволинейного движения материальной точки является составление кинематического уравнения, описывающего это движение и позволяющего по заданным начальным условиям определить все характеристики этого движения.
Материальная точка движется по кривой, представленной на рис.4. Центры окружностей О1, О2, О3 лежат на одной прямой. Определить перемещение $\left|\overrightarrow{s}\right|$ и длину пути l при движении из точки А в точку В.
Решение
Центры окружностей лежат на одной прямой, поэтому
Траектория представляет собой сумму полуокружностей:
Зависимость пройденного телом пути от времени задается уравнением $s(t) = A + Bt + Ct^2 + Dt^3 \ \ (C = 0,1 м/с^2, D = 0,03 м/с^3)$. Определите, через сколько времени после начала движения ускорение тела будет равно $2 м/с^2$.
Решение