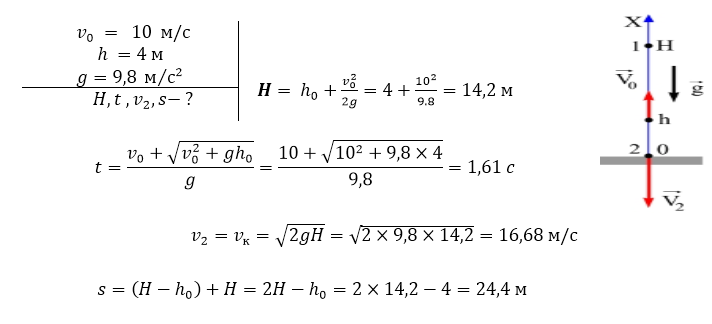Тело, брошенное вертикально вверх с начальной скоростью $v_0$, движется равнозамедленно с ускорением $a=-g=-9,81\ {v}/{c^2}$.
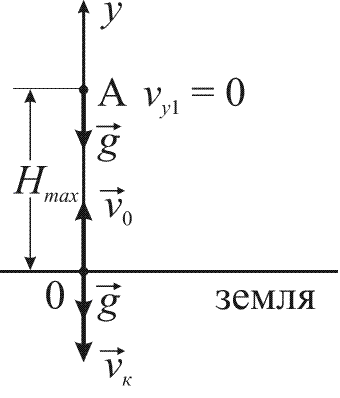
Рисунок 1
Высота подъема $h$ за время $t$ и скороcть $v$ через время $t$ определяются формулами:
Время $t_max$, за которое тело достигнет максимальной высоты $h_max = h$, при которой $v = 0$, и высота $h_max$ определяются формулами:
Тело, достигшее высоты $h_max$, имеет скорость $v = 0$ и ускорение $g$. Поэтому оно не останется на достигнутой высоте, а переходит в состояние свободного падения. Таким образом, движение тела, брошенного вверх - есть сложное равнозамедленное движение, при котором после достижения высоты $h_max$ знаки перемещения и скорости меняются на противоположные. При этом важно, с какой начальной высоты $h_0$ это движение начиналось. Обозначив общее время движения тела равным $t$, время свободного падения на землю $t_п$, конечную скорость $v_к$, получим:
Для случая, когда тело брошено вертикально вверх от уровня земли, $h_0=0$
Время падения тела до высоты, с которой оно было брошено вертикально вверх, равно времени его подъёма на максимальную высоту.
Учитывая, что в наивысшей точке скорость равна нулю
получим:
Конечная скорость $v_к$ тела, брошенного от уровня земли вертикально вверх, будет равна начальной скорости $v_0$ по величине и противоположна по направлению. (рис.2.)
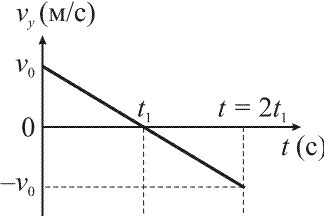
Рисунок 2
С высоты 25 м тело брошено вертикально вверх со скоростью 15 м/с. Через сколько секунд оно упадет на землю?
Решение:
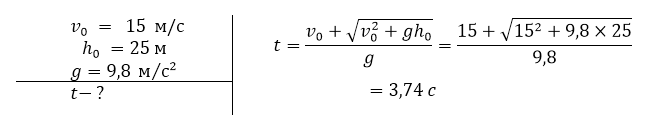
С высоты h=4 м над поверхностью Земли бросили камень вертикально вверх с начальной скоростью V0=10 м/с. Определить: максимальную высоту, на которую поднимется камень, время полета камня и скорость с которой он упадет на Землю. Определить путь, пройденный телом.
Решение