
Что такое изобарический процесс
Изобарическим (или изобарным) процессом называется процесс, происходящий в неизменной массе газа при постоянном давлении.
Запишем уравнение для двух состояний идеального газа:
\[pV_1=\nu RT_1\left(1\right),\] \[pV_2=\nu RT_2\ \left(2\right).\]Разделим уравнение (2) на уравнение (1), получим уравнение изобарного процесса:
\[\frac{V_2}{V_1}=\frac{T_2}{T_1}\ (3)\]или
\[\frac{V}{T}=const\ \left(4\right).\]Уравнение (4) называют законом Гей-Люссака.
Внутренняя энергия и количество теплоты изобарического процесса
Этот процесс происходит с подводом тепла, если объем увеличивается, или его отводом, чтобы уменьшать объем. Запишем первое начало термодинамики, последовательно получим выражения для работы, внутренней энергии и количества теплоты изобарного процесса:
\[\delta Q=dU+dA=\frac{i}{2}\nu RdT+pdV,\ \left(5\right).\] \[\triangle Q=\int\limits^{T_2}_{T_1}{dU}+\int\limits^{V_2}_{V_1}{dA}(6)\]где $\delta Q\ $- элементарное тепло, подводимое к системе, $dU$- изменение внутренней энергии газа в проводимом процессе, $dA$- элементарная работа, которую совершает газ в процессе, i-число степеней свободы молекулы газа, R -- универсальная газовая постоянная, d - количество молей газа.
Изменение внутренней энергии газа:
\[\triangle U=\frac{i}{2}\nu R{(T}_2-T_1)\ (7)\] \[A=p\int\limits^{V_2}_{V_1}{dV}=p\left(V_2-V_1\right)(8)\]Уравнение (8) определяет работу для изобарного процесса. Вычтем из (2) уравнение (1), получим еще одно уравнение для работы газа в изобарном процессе:
\[p{(V}_2-V_1)=\nu R{(T}_2-T_1)\to A=\nu R{(T}_2-T_1)\ (9)\] \[\triangle Q=\frac{i}{2}нR{(T}_2-T_1)+\nu R{(T}_2-T_1)=c_{\mu p}\nu \triangle T\ (10),\]где $c_{\mu p}$ -- молярная теплоёмкость газа при изобарном процессе. Уравнение (10) определяет количество теплоты, сообщаемое газу массы m в изобарном процессе при увеличении температуры на $\triangle T.$
Изопроцессы очень часто изображают на термодинамических диаграммах. Так, линия, изображающая на такой диаграмме изобарический процесс, называется изобарой (рис.1).
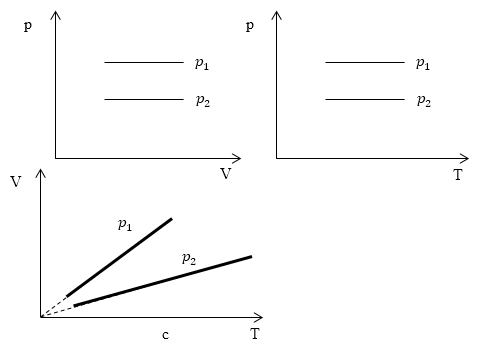
Рис. 1
Задание: Определите, как соотносятся давления $p_1$ и $p_2$ на диаграмме V(T) рис 1с.
Решение:
Проведем изотерму $T_1$
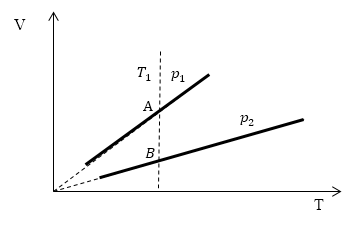
Рис. 2
В точках А и В температуры одинаковы, следовательно, газ подчиняется закону Бойля -- Мариотта:
\[p_AV_A=p_BV_B\ (1.2)\] \[V_A > V_B\to p_A Ответ: Давления $p_1 > p_2$.Задание: При неизменном давлении p=3$\cdot {10}^5$Па газ расширился от объема $V_1=2л$ до $V_2=4л.$ Найти работу, совершаемую газом.
Решение:
За основу решения задачи примем формулу работы при расширении газа в изобарном процессе:
\[A=p\int\limits^{V_2}_{V_1}{dV}=p\left(V_2-V_1\right)\left(2.1\right).\]Переведем данные объемы в СИ: $V_1=2л=2{\cdot 10}^{-3}м^3$, $V_2=4л=4{•10}^{-3}м^3$
Проведем вычисления:
\[A=3\cdot {10}^5\left(4-2\right){•10}^{-3}=600(Дж)\]Ответ: Работа газа в изобарном процессе 600 Дж.
Задание: Сравните работу газа в процессе ABC и работу над газом в процессе CDA рис 3.
Решение:
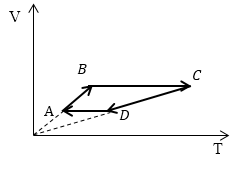
Рис. 3
За основу решения примем формулу, определяющую работу газа:
\[A=\int\limits^{V_2}_{V_1}{pdV}(3.1)\]Из геометрического смысла определенного интеграла известно, что работа -- есть площадь фигуры, которая ограничена функцией подынтегрального выражения, осью абсцисс, и изохорами в точках $V_1\ и\ V_2$ (оси p(V)). Переведем графики процессов в оси p(V).
Рассмотрим каждый отрезок графиков процессов изображенных на рисунке (3).
АВ: Изохорный процесс (p=const), $V\uparrow \left(\ Объем\ растет\right),\ T\uparrow $;
ВС: Изохорный процесс (V =const), $T\uparrow $ (из графика), p$\uparrow $, из закона для изохорного процесса ($\frac{p}{T}=const$);
CD: (p=const), $V\downarrow ,\ T\downarrow ;$
DA: (V =const), $T\downarrow ,\ p\downarrow .$
Изобразим графики процессов в осях p(V) (рис.4):
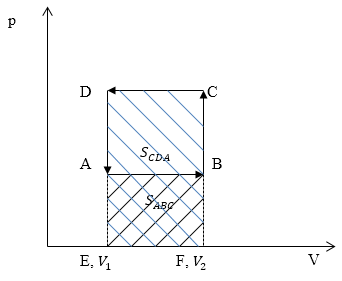
Рис. 4
Работа газа $A_{ABC}=S_{ABC}$ ($S_{ABC}$ -- площадь прямоугольника ABFE) (рис. 3). Работа над газом $A_{CDA}=S_{CDA}$ ($S_{CDA}$)$\ -площадь\ прямоугольника\ $EFCD.Очевидно, что $A_{CDA}>A_{ABC}.$
Ответ: $A_{CDA}>A_{ABC}.$











