
В случае равновесного распределения заряды проводника распределяются в тонком поверхностном слое. Так, например, если проводнику сообщить отрицательный заряд, то из-за наличия сил отталкивания элементов этого заряда они рассредоточатся по всей поверхности проводника.
Исследование при помощи пробной пластинки
Для того чтобы на опыте исследовать, как распределяются заряды на внешней поверхности проводника используют так называемую пробную пластинку. Эта пластинка настолько мала, что при соприкосновении с проводником ее можно рассматривать как часть поверхности проводника. Если эту пластинку приложить к заряженному проводнику, то часть заряда ($\triangle q$) перейдет на нее и величина этого заряда будет равна заряду, который находился на поверхности проводника по площади равной площади пластинки ($\triangle S$).
Тогда величина равная:
\[\sigma=\frac{\triangle q}{\triangle S}(1)\]называется поверхностной плотностью распределения заряда в данной точке.
Разряжая пробную пластинку через электрометр можно судить о величине поверхностной плотности заряда. Так, например, если зарядить проводящий шар, то можно увидеть, с помощью вышеприведенного метода, что в состоянии равновесия поверхностная плотность заряда на шаре одна и та же во всех его точках. То есть заряд по поверхности шара распределяется равномерно. Для проводников более сложной формы распределение заряда сложнее.
Поверхностная плотность проводника
Поверхность любого проводника является эквипотенциальной, но в общем случае плотность распределения заряда может очень сильно отличаться в разных точках. Поверхностная плотность распределения заряда зависит от кривизны поверхности. В разделе, который был посвящен описанию состояния проводников в электростатическом поле, мы установили, что напряженность поля около поверхности проводника перпендикулярна поверхности проводника в любой его точке и равна по модулю:
\[E=\frac{\sigma}{\varepsilon {\varepsilon }_0}\ \left(2\right),\]где ${\varepsilon }_0$ -- электрическая постоянная, $\varepsilon $ -- диэлектрическая проницаемость среды. Следовательно,
\[\sigma=E\varepsilon {\varepsilon }_0\ \left(3\right).\]Чем больше кривизна поверхности тем, тем больше напряженность поля. Следовательно, на выступах плотность заряда особенно велика. Вблизи углублений в проводнике эквипотенциальные поверхности расположены реже. Следовательно, напряженность поля и плотность зарядов в этих местах меньше. Плотность зарядов при заданном потенциале проводника определяется кривизной поверхности. Она растет с увеличением выпуклости и убывает с увеличением вогнутости. Особенно большая плотность заряда на остриях проводников. Так, напряженность поля на острие может быть настолько велика, что может возникать ионизация молекул газа, который окружает проводник. Ионы газа противоположного знака заряда (относительно заряда проводника) притягиваются к проводнику, нейтрализуют его заряд. Ионы того же знака отталкиваются от проводника, «тянут» за собой нейтральные молекулы газа. Такое явление называют электрическим ветром. Заряд проводника уменьшается в результате процесса нейтрализации, он как бы стекает с острия. Такое явление называют истечением заряда с острия.
Мы уже говорили, что когда мы вносим проводник в электрическое поле, происходит разделение положительных зарядов (ядер) и отрицательных (электронов). Такое явление носит название электростатической индукции. Заряды, которые появляются в результате, называют индуцированными. Индуцированные заряды создают дополнительное электрическое поле.
Поле индуцированных зарядов направлено в сторону противоположную направлению внешнего поля. Поэтому заряды, которые накапливаются на проводнике, ослабляют внешнее поле.
Перераспределение зарядов идет, пока не выполнены условия равновесия зарядов для проводников. Такие как: равенство нулю напряженности поля везде внутри проводника и перпендикулярность вектора напряженности заряженной поверхности проводника. Если в проводнике есть полость, то при равновесном распределении индуцированного заряда поле внутри полости равно нулю. На этом явлении основана электростатическая защита. Если какой-либо прибор хотят защитить от воздействия внешних полей, его окружают проводящим экраном. В таком случае внешнее поле компенсируется внутри экрана возникающими на его поверхности индуцированными зарядами. Такой может быть не обязательно сплошным, но и в виде густой сетки.
Задание: Бесконечно длинная нить, заряженная с линейной плотностью $\tau $, расположена перпендикулярно бесконечно большой проводящей плоскости. Расстояние от нити до плоскости $l$. Если продолжить нить до пересечения с плоскостью, то в месте пересечения получим некоторую точку А. Составьте формулу зависимости поверхностной плотности $\sigma \left(r\right)\ $индуцированных зарядов на плоскости от расстояния до точки А.
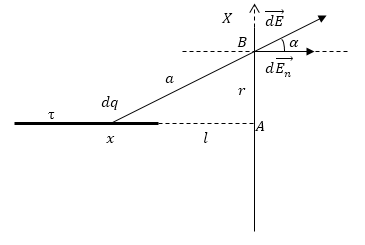
Рис. 1
Решение:
Рассмотрим некоторую точку В на плоскости. Бесконечно длинная заряженная нить в точке В создает электростатическое поле, в поле находится проводящая плоскость, на плоскости образуются индуцированные заряды, которые в свою очередь создают поле, которое ослабляет внешнее поле нити. Нормальная составляющая поля плоскости (индуцированных зарядов) в точке В будет равна нормальной составляющей поля нити в этой же точке, если система находится в равновесии. Выделим на нити элементарный заряд ($dq=\tau dx,\ где\ dx-элементарный\ кусочек\ нити\ $), найдем в точке В напряжённость, создаваемую этим зарядом ($dE$):
\[dE=\frac{\tau dx}{4\pi {\varepsilon }_0\varepsilon a^2}\left(1.1\right).\]Найдем нормальную составляющую элемента напряженности поля нити в точке В:
\[dE_n=dEcos\alpha =\frac{\tau dxcos\alpha }{4\pi {\varepsilon }_0\varepsilon a^2}\left(1.2\right),\]где $cos\alpha $ выразим как:
\[cos\alpha =\frac{x}{a}\left(1.3\right).\]Выразим расстояние $a$ по теореме Пифагора как:
\[a=\sqrt{r^2+x^2}\ \left(1.4\right).\]Подставим (1.3) и (1.4) в (1.2), получим:
\[dE_n=\frac{\tau dx}{4\pi {\varepsilon }_0\varepsilon a^2}\frac{x}{a}=\frac{\tau xdx}{4\pi {\varepsilon }_0\varepsilon {\left(r^2+x^2\right)}^{{3}/{2}}}\left(1.5\right).\]Найдем интеграл от (1.5) где пределы интегрирования от $l\ (расстояние\ до\ ближайшего\ конца\ нити\ от\ плоскости)\ до\ \infty $:
\[E_n=\int\limits^{\infty }_l{\frac{\tau xdx}{4\pi {\varepsilon }_0\varepsilon {\left(r^2+x^2\right)}^{{3}/{2}}}}=\frac{\tau }{4\pi {\varepsilon }_0\varepsilon }\int\limits^{\infty }_l{\frac{xdx}{{\left(r^2+x^2\right)}^{{3}/{2}}}}=\frac{\tau }{4\pi {\varepsilon }_0\varepsilon }\cdot \frac{1}{{\left(r^2+x^2\right)}^{{1}/{2}}}\left(1.6\right).\]С другой стороны, мы знаем, что поле равномерно заряженной плоскости равно:
\[E=\frac{\sigma}{2\varepsilon {\varepsilon }_0}\ \left(1.7\right).\]Приравняем (1.6) и (1.7), выразим поверхностную плотность заряда:
\[\frac{1}{2}\cdot \frac{\sigma}{\varepsilon {\varepsilon }_0}=\frac{\tau }{4\pi {\varepsilon }_0\varepsilon }\cdot \frac{1}{{\left(r^2+x^2\right)}^{{1}/{2}}}\to \sigma=\frac{\tau }{2\cdot \pi {\left(r^2+x^2\right)}^{{1}/{2}}}.\]Ответ: $\sigma=\frac{\tau }{2\cdot \pi {\left(r^2+x^2\right)}^{{1}/{2}}}.$
Задание: Рассчитайте поверхностную плотность заряда, который создается около поверхности Земли, если напряженность поля Земли равна 200$\ \frac{В}{м}$.
Решение:
Будем считать, что диэлектрическая проводимость воздуха $\varepsilon =1$ как у вакуума. За основу решения задачи примем формулу для расчёта напряженности заряженного проводника:
\[E=\frac{\sigma}{\varepsilon {\varepsilon }_0}\left(2.1\right).\]Выразим поверхностную плотность заряда, получим:
\[\sigma=E{\varepsilon }_0\varepsilon \ \left(2.2\right),\]где электрическая постоянная нам известна и равна в СИ ${\varepsilon }_0=8,85\cdot {10}^{-12}\frac{Ф}{м}.$
Проведем вычисления:
\[\sigma=200\cdot 8,85\cdot {10}^{-12}=1,77\cdot {10}^{-9}\frac{Кл}{м^2}.\]Ответ: Поверхностная плотность распределения заряда поверхности Земли равна $1,77\cdot {10}^{-9}\frac{Кл}{м^2}$.











