
Потоком вектора $\overrightarrow{a}\ $через поверхность $S$ называют алгебраическую величину${\ Ф}_a$, которая определяется следующим образом:
\[Ф_a=\int\limits_S{\overrightarrow{a}d\overrightarrow{S}}\ \left(1\right).\]При этом знак потока зависит от выбора направления нормали к элементарной площадке $dS$.
Элементарный поток вектора напряженности
Обратимся к электрическому полю. Модуль напряженности равен количеству силовых линий, которые пересекают поверхность площадь, которой равна единице, причем поверхность должна быть перпендикулярна линиям поля в данном месте. Количество линий поля, которые пересекают вышеназванную поверхность, называются потоком вектора напряженности. Если выделить элементарную площадку поверхности (dS), построить нормаль к этой площадке $\overrightarrow{n}$, при этом угол между направлением вектора нормали и направлением вектора напряженности составит $\alpha $, то элементарный поток вектора напряженности ($dФ_E$) можно записать как:
\[dФ_E=EdScos\alpha =\overrightarrow{E}\cdot d\overrightarrow{S}\ \left(2\right),\]где
\[d\overrightarrow{S}=\overrightarrow{n}dS\ \left(3\right).\]В уравнении (3) $\overrightarrow{n}$ единичная нормаль к площадке $dS$.
Если рассматривать какую -- либо произвольную поверхность $S$, то в соответствии с определением потока вектора (1) можно записать, что поток вектора напряженности ($Ф_E$):
\[Ф_E=\int\limits_S{\overrightarrow{E}\cdot d\overrightarrow{S}}\ \ \left(4\right).\]Направление нормали
Как и в общем случае, поток вектора напряженности алгебраическая величина. Знак потока зависит от конфигурации поля и направления вектора - нормали $\overrightarrow{n}$. Направление нормали условно. Можно сказать, что интеграл в уравнении (4) характеризует суммарную мощность источников вектора $\overrightarrow{E}$, коими являются заряды, внутри объема, который ограничивает поверхность $S$.
Принято считать, что если имеют дело с замкнутой поверхностью, то нормаль имеет положительное направление наружу. Поток вектора напряженности в случае замкнутой поверхности записывают через криволинейный интеграл по замкнутой поверхности:
\[Ф_E=\oint\limits_S{\overrightarrow{E}\cdot d\overrightarrow{S}}\ \ \left(5\right).\]Задание: Напряженность электростатического поля задана формулой в декартовых координатах:
\[\overrightarrow{E}=\frac{x\overrightarrow{i}+y\overrightarrow{j}}{x^2+y^2},\]где $\overrightarrow{i},\ \overrightarrow{j}$ -- единичные орты осей OX и OY. Найдите поток вектора $\overrightarrow{E}$ через сферическую поверхность, если ее радиус равен $R$, а ее центр находится в начале координат.
Решение:
В качестве основы для решения используем определение потока вектора напряженности, а именно:
\[Ф_E=\int\limits_S{\overrightarrow{E}\cdot d\overrightarrow{S}}\ \ \left(1.1\right),\ \]где $d\overrightarrow{S}=\overrightarrow{n}dS$, $dS-$ элементарный участок поверхности сферы, $\overrightarrow{n}$ -- нормаль к этому участку.
Запишем выражение для нормали к поверхности сферы, в виде:
\[\overrightarrow{n}=\frac{x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}}{\sqrt{x^2+y^2+z^2}}\ \left(1.2\right).\]Подставим уравнение (1.2) в (1.1), используем выражение для напряжённости поля из условий задачи, найдем интеграл, при этом при нахождении произведения в подынтегральном выражении, учитываем, что $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$- ортогональные единичные векторы.
\[Ф_E=\int\limits_S{\overrightarrow{E}\cdot \overrightarrow{n}dS}=\int\limits_S{\frac{x\overrightarrow{i}+y\overrightarrow{j}}{x^2+y^2}\cdot \frac{x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}}{\sqrt{x^2+y^2+z^2}}dS}=\int\limits_S{\frac{x^2+y^2}{x^2+y^2\sqrt{x^2+y^2+z^2}}}\ dS=\int\limits_S{\frac{dS}{\sqrt{R^2}}}=\frac{1}{R}\ \int\limits_S{dS=\frac{4\pi R^2}{R}}=4\pi R.\]Ответ: $Ф_E=4\pi R.$
Задание: Определите поток вектора напряженности через поверхность сферы, если внутри нее находится два точечных заряда $+q_1$ и ${-q}_2$.
Решение:
В качестве основы для решения можно взять формулу для потока вектора напряженности в виде:
\[Ф_E=\overrightarrow{E}\cdot S\overrightarrow{n}=EScos\alpha \ \left(2.1\right),\]где $\alpha $ -- угол между нормалью к поверхности, через который ищем поток и вектором напряженности. Поле точечного заряда имеет сферическую симметрию (рис.1). Следовательно, вектор напряженности поля и вектор - нормаль будут сонаправлены ($cos\alpha ={cos 0\ }=1$). На рис. 1 изображено поле положительного заряда.
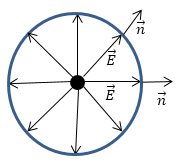
Рис. 1
Результирующая напряженность поля может быть найдена в соответствии с принципом суперпозиции полей двух зарядов, с учетом знаков.
Запишем выражение для модуля напряженности поля, которое создает первый заряд:
\[E_1=k\frac{q_1}{r^2}\left(2.2\right).\]Для второго заряда:
\[E_2=k\frac{q_2}{r^2}\left(2.3\right).\]Найдем модуль результирующей напряженности, учитывая, что положительный заряд -- исток поля, а отрицательный -- сток поля, то есть направления полей противоположны:
\[E=E_1-E_2=k\frac{q_1}{r^2}-k\frac{q_2}{r^2}\ \left(2.4\right).\]Если мы ищем поток через сферу, которая имеет радиус R, то выражение (2.4) примет вид:
\[E=k\frac{q_1-q_2}{R^2}\ \left(2.5\right).\]Площадь поверхности сферы (S) заданного радиуса равна:
\[S=4\pi R^2\left(2.6\right).\]В таком случае, подставим выражения (2.6) и (2.5) в (2.1), учтем, что $cos\alpha ={cos 0\ }=1$, получим:
\[Ф_E=k\frac{q_1-q_2}{R^2}\ 4 \pi R^2=\frac{q_1-q_2}{4\pi {\varepsilon }_0R^2}4 \pi R^2=\frac{q_1-q_2}{\varepsilon_0}.\]Ответ: $Ф_E=\frac{q_1-q_2}{{\varepsilon }_0}.$











