Формула потенциальной энергии
Обратимся вновь к рассмотрению полярных диэлектриков. Дипольный момент $\overrightarrow{p}$, молекулы, которая находится в электрическом поле с напряженностью $\overrightarrow{E,}\ $имеет потенциальную энергию, которая вычисляется по формуле:
Величина $W$ достигает минимального значения в том случае, когда $\overrightarrow{p}\uparrow \uparrow \overrightarrow{E.}$ Так как устойчивым состоянием системы является состояние с минимумом потенциальной энергии, то моменты диполей стремятся повернуться до совпадения с направлением напряженности поля. Этот поворот осуществляет пара сил, которые действуют на диполь в электрическом поле. Тепловое движение, в свою очередь, мешает упорядочивающему действию электрического поля. В результате устанавливается равновесие.
Направим ось Z вдоль вектора напряженности электрического поля (рис. 1).
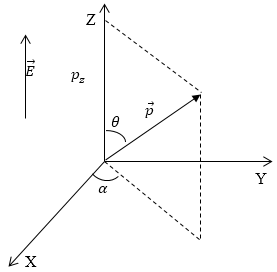
Рис. 1
В таком случае формулу (1) запишем в виде:
В данном случае можно использовать распределение Больцмана, которое будет характеризовать распределение направлений дипольных моментов молекул по углам. Количество молекул $dn$, дипольные моменты которых расположены в телесном угле $d\Omega $ при этом будет равно:
В таком случае среднее z-компоненты дипольного момента ($\left\langle p_z\right\rangle $) равно:
где $\beta =\frac{pE}{kT}$, $k$ -- постоянная Больцмана, $T$ -- термодинамическая температура. Вычислим интеграл $(I)$:
Интеграл в числители дроби выражения (4) можно представить как:
Тогда возьмем производную по $\beta \ $от результата интегрирования (5), мы имеем:
Функция Ланжевена
В таком случае используя результаты (6) и (7) перепишем формулу (4), получим:
\[\left\langle p_z\right\rangle =pL\left(\beta \right)=p\left(cth\beta -\frac{1}{\beta }\right)\ \left(8\right),\]где $L\left(\beta \right)=cth\beta -\frac{1}{\beta }$ -- функция Ланжевена. Ее график изображен на рис. 2
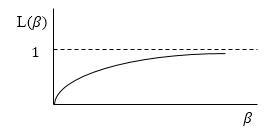
Рис. 2
Задание: Используя функцию Ланжевена, найдите среднюю величину проекции дипольного момента на ось Z в ортогональной системе координат ($\left\langle p_z\right\rangle $) при условии низкой напряженности поля.
Решение:
За основу примем формулу, которая связывает $\left\langle p_z\right\rangle $ с функцией Ланжевена, а именно:
\[\left\langle p_z\right\rangle =pL\left(\beta \right)=p\left(cth\beta -\frac{1}{\beta }\right)\ \left(1.1\right).\]При небольших напряженностях поля ($pE\ll kT$), то есть $\beta \ll 1$ гиперболический котангенс можно разложить в ряд:
\[cth\beta =\frac{1}{\beta }+\frac{\beta }{3}-\frac{{\beta }^3}{45}+\dots \left(1.2\right).\]Ограничимся в функции Ланжевена двумя первыми членами, тогда она будет иметь вид:
\[L\left(\beta \right)=\frac{1}{\beta }+\frac{\beta }{3}-\frac{1}{\beta }=\frac{\beta }{3}\left(1.3\right).\]В таком случае следуя формуле (1.1) получаем:
\[\left\langle p_z\right\rangle =p\frac{в}{3}=\frac{p}{3}\frac{pE}{kT}=\frac{p^2E}{3kT}\left(1.4\right).\]Ответ: При $pE\ll kT$, $\left\langle p_z\right\rangle =\frac{p^2E}{3kT}$.
Задание: Используя функцию Ланжевена, объясните, что происходит в диэлектрике с увеличением напряжённости поля. Рассмотрите случай, при котором $pE\gg kT.$
Решение:
При увеличении напряженности поля, дипольные моменты все более интенсивно ориентируются в направлении вектора напряженности поля и в случае, если $pE\gg kT$ то есть $\beta =\frac{pE}{kT}\gg 1$, можно полагать, что все дипольные моменты параллельны между собой и имеют направление совпадающее с направлением вектора напряженности. Значит, что:
\[\left\langle p_z\right\rangle =p\ \left(2.1\right),\]где $p_z$ -- проекция вектора дипольного момента молекулы на ось Z. Это условие легко получить из соотношения:
\[\left\langle p_z\right\rangle =pL\left(\beta \right)=p\left(cth\beta -\frac{1}{\beta }\right)\ \left(2.3\right)\]если $\beta \gg 1,\ $то функция Ланжевена стремится к единице (рис.2):
\[L\left(\beta \to \infty \right)\to 1\ \left(2.4\right).\]Напомним, что
\[cth\beta =\frac{e^{2\beta }+1}{e^{2\beta }-1}\ \left(2.5\right).\] \[{\mathop{lim}_{\beta \to \infty } cth\beta \ }=\mathop{lim}_{\beta \to \infty }\left(\frac{e^{2\beta }+1}{e^{2\beta }-1}\right)=\mathop{lim}_{\beta \to \infty }\left(\frac{e^{2\beta }}{e^{2\beta }-1}\right)+\mathop{lim}_{\beta \to \infty }\left(\frac{1}{e^{2\beta }-1}\right)\left(2.6\right).\] \[\mathop{lim}_{\beta \to \infty }\left(\frac{1}{e^{2\beta }-1}\right)=0\ \left(2.7\right).\] \[\mathop{lim}_{\beta \to \infty }\left(\frac{e^{2\beta }}{e^{2\beta }-1}\right)=\mathop{lim}_{\beta \to \infty }\left(\frac{1}{\frac{e^{2\beta }}{e^{2\beta }}-\frac{1}{e^{2\beta }}}\right)=\mathop{lim}_{\beta \to \infty }\left(\frac{1}{1-\frac{1}{e^{2\beta }}}\right)=1\ \left(2.8\right).\]Учитывая (2.7) и (2.8) получим:
\[{\mathop{lim}_{\beta \to \infty } cth\beta \ }=1\ \left(2.9\right).\]При выполнении условия (2.1) достигается максимально возможная поляризованность и увеличение напряженности поля не ведет к увеличению поляризованности. Напряженность поля, при которой достигается максимальная поляризация, называется напряженностью поля насыщения.












