Заряды конденсатора
Электрическая энергия, как и любой другой вид энергии, зависит исключительно от состояния системы, и не зависит от способа, которым данная система пришла в такое состояние.
Электрическая энергия заряженного конденсатора зависит от заряда (q), который находится на его обкладках или напряжением между ними (U).
Каким образом конденсатор был заряжен, не влияет на энергию, запасенную в нем. Допустим, что изначально конденсатор не заряжен. Это значит, что на каждой из его обкладок есть и положительный заряд и отрицательный, они одинаковы, и в результате суммарный заряд проводников равен нулю. Станем заряжать конденсатор небольшими порциями dq, перенося порции заряда с отрицательной обкладки на положительную. На практике это осуществляется с помощью соединения обкладок конденсатора проводом, в котором включён источник ЭДС. Источник ЭДС перекачивает заряд до тех пор пока разность потенциалов обкладок не достигнет заданной величины. Весь этот процесс означает, что внешние по отношению к полю конденсатора силы совершают работу ($\delta A^{vnesh}$) против сил поля равную:
\[\delta A^{vnesh}=({\varphi }_1-{\varphi }_2)dq\ \left(1\right),\]где ${\varphi }_1-{\varphi }_2=U$ -- разность потенциалов между обкладками. Работа сил поля ($\delta A$) самого конденсатора при этом равна:
\[\delta A=-\delta A^{vnesh}=-({\varphi }_1-{\varphi }_2)dq\left(2\right).\]Зарядка конденсатора
Зарядка конденсатора может сопровождаться выделением или поглощением тепла, изменением плотности диэлектрика. В данном случае будем считать эти эффекты не существенными. Это значит, что мы будем считать, что диэлектрическая проницаемость постоянна ($\varepsilon =const).\ $В таком случае вся работа внешних сил пойдет на увеличение электрической энергии конденсатора (W). В таком случае мы можем записать:/p> \[dW=({\varphi }_1-{\varphi }_2)dq=\frac{qdq}{C}\ \left(3\right).\]
Мы уже сказали, что в процессе зарядки конденсатора $\varepsilon =const$, следовательно, не изменится емкость конденсатора. Проинтегрируем уравнение (3), получим, что:
\[W=\frac{q^2}{2C}\ \left(4\right).\]Или зная связь заряда, емкости и потенциала проводника:
\[C=\frac{q}{{\varphi }_1-{\varphi }_2}=\frac{q}{U}(5)\]выражение (4) можно записать как:
\[W=\frac{qU}{2C}=\frac{1}{2}CU^2\ \left(6\right).\]Задание: Два конденсатора имеют емкости $C_1\ и\ C_2$. Они заряжены до напряжений $U_1\ и\ U_2$ соответственно. Конденсаторы соединили параллельно. Определите, какое количество тепла выделится при таком соединении?
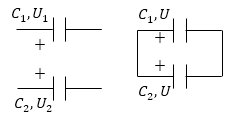
Рис. 1
Решение:
Потенциалы обкладок, которые соединили стали одинаковыми. По закону сохранения сумма заряда на обкладках конденсаторов сохранилась.
Значит можно записать следующее:
\[q_1+q_2=\widetilde{q_1}+\widetilde{q_2}\left(1.1\right),\]где $q_1; q_2$ заряды конденсаторов до того как их соединили, соответственно $\widetilde{q_1};;\widetilde{q_2}$ - заряды конденсаторов после их соединения. Причем:
\[q_1=C_1U_1,\] \[q_2=C_2U_2\ \left(1.2\right).\]Количество тепла, которое выделится при соединении конденсаторов равно:
\[Q=W_1-W_2\left(1.3\right),\]где $W_1$ -- суммарная энергия конденсаторов до соединения, $W_2$ -- сумма энергий полей конденсаторов после соединения. Причем:
\[W_1=\frac{1}{2}\left(C_1{U_1}^2+C_2{U_2}^2\right)\left(1.4\right).\] \[W_2=\frac{С U^2}{2}\ \left(1.5\right).\]Подставим (1.5) и (1.4) в уравнение (1.3), получим:
\[Q=\frac{1}{2}\left(C_1{U_1}^2+C_2{U_2}^2\right)-\frac{СU^2}{2}\ \left(1.6\right).\]Емкость параллельного соединения конденсаторов (С) найдем как:
\[С=C_1+C_2\left(1.7\right).\]Если уравнение (1.1) переписать, заменив заряды, на соответствующие произведения емкостей и разностей потенциалов, то получим:
\[C_1U_1+C_2U_2=C_1U+C_2U\ \left(1.8\right).\]Выразим из (1.8) разность потенциалов на конденсаторах после их соединения:
\[\frac{C_1U_1+C_2U_2}{C_1+C_2}=U\ \left(1.9\right).\]Подставим (1.9) в (1.6) найдем искомую теплоту:
\[Q=\frac{C_1C_2{\left(U_1-U_2\right)}^2}{2{(C}_1+C_2)}.\]Ответ: $Q=\frac{C_1C_2{\left(U_1-U_2\right)}^2}{2{(C}_1+C_2)}.$
Задание: Площадь обкладок плоского воздушного конденсатора равна $S$. Какую работу следует совершить, чтобы увеличить расстояние между обкладками конденсатора от $d_1$ до $d_2$. Если при этом постоянным поддерживается разность потенциалов (U) на конденсаторе. Процесс проводится медленно.
Решение:
Процесс проводится медленно, будем считать, что выделения тепла в системе не происходит, в таком случае изменение внутренней энергии конденсатора равно работе по перемещению обкладок, то есть запишем:
\[A=W_2-W_1\ \left(2.1\right).\]Если неизменным остается напряжение на обкладках конденсатора в ходе наших манипуляций, а изменение энергии поля конденсатора происходит за счет изменения емкости, то выражение для энергии поля удобнее использовать в виде:
\[W=\ \frac{1}{2}CU^2\ \left(2.2\right).\]В таком случае имеем:
\[A=\frac{1}{2}U^2\left(C_2-C_1\right)\left(2.3\right),\]где $C_2,C_1$ -- емкости конденсатора до увеличения и после увеличения расстояния между обкладками. Емкость плоского конденсатора может быть найдена по формуле:
\[C=\frac{\varepsilon {\varepsilon }_0S}{d}\left(2.4\right),\]где $\varepsilon $=1, так как по условию задачи конденсатор воздушный. Используем (2.4), подставим в (2.3) выражения для емкостей конденсатора в двух заданных состояниях, получим:
\[A=\frac{1}{2}U^2\left(\frac{\varepsilon {\varepsilon }_0S}{d_2}-\frac{\varepsilon {\varepsilon }_0S}{d_1}\right)=\frac{1}{2}U^2\varepsilon {\varepsilon }_0S\left(\frac{d_2-d_1}{d_2d_1}\right).\]Ответ: $A=\frac{1}{2}U^2\varepsilon {\varepsilon }_0S\left(\frac{d_2-d_1}{d_2d_1}\right).$












