Емкость плоского и других конденсаторов

Конфигурация конденсатора такова, что поле, которое создается зарядами, локализовано между обкладками. В общем случае электроемкость конденсатора равна:

$$C=\frac{q}{{\varphi }_1-{\varphi }_2}=\frac{q}{U}\left(1\right),$$

где ${\varphi }_1-{\varphi }_2=U$ -- разность потенциалов обкладок, которую называют напряжением и обозначают $U$. Емкость по определению считается положительной величиной. Она зависит только от геометрии обкладок конденсатора их взаиморасположения и диэлектрика. Форму обкладок и их расположение подбирают так, чтобы внешние поля минимально влияли на внутреннее поле конденсатора. Силовые линии поля конденсатора начинались на проводнике с положительным зарядом и заканчивались на проводнике с отрицательным зарядом. Конденсатор может быть проводником, который помещен в полость, окруженную замкнутой оболочкой.

В соответствии с конфигураций конденсаторов можно выделить три большие группы: плоские, сферические и цилиндрические (по форме обкладок). Вычисление емкости конденсатора сводится к определению $напряжения$ конденсатора при известном заряде на его обкладках.

Плоский конденсатор

Плоский конденсатор (рис.1) - это две разноименно заряженные пластины, разделенные тонким слоем диэлектрика. Формула для расчета емкости такого конденсатора представляет собой выражение:

$$С=\frac{\varepsilon {\varepsilon }_0S}{d}\left(2\right),$$

где $S$ -- площадь обкладки, $d$ -- расстояние между обкладками, $\varepsilon$ -- диэлектрическая проницаемость вещества. Чем меньше $d$, тем больше совпадает расчётная емкость конденсатора (2), с реальной емкостью.

Рис. 1

Электроемкость плоского конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равна $d_i$, диэлектрическая проницаемость этого слоя ${\varepsilon }_i$ вычисляется по формуле:

$$C=\frac{{\varepsilon }_0S}{\frac{d_1}{{\varepsilon }_1}+\frac{d_2}{{\varepsilon }_2}+\dots +\frac{d_N}{{\varepsilon }_N}}\ \left(3\right).$$

Сферический конденсатор

В том случае, если внутренний проводник шар или сфера, внешняя замкнутая оболочка -- концентрическая ему сфера, то конденсатор является сферическим. Сферический конденсатор (рис.2) состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком. Емкость его можно рассчитать по формуле:

$$C=4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}\ \left(4\right),$$

где $R_1{\ и\ R}_2$ -- радиусы обкладок.

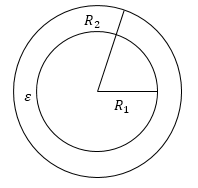
Рис. 2

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равна:

$$C=\frac{2\pi \varepsilon {\varepsilon }_0l}{{ln \left({R_2}/{R_1}\right)\ }}\left(5\right),$$

где $l$ - высота цилиндров, $R_1$ и $R_2$ -- радиусы обкладок. Этот вид конденсаторов представляет собой две коаксиальных (соосных) проводящих цилиндрических поверхности (рис.3).

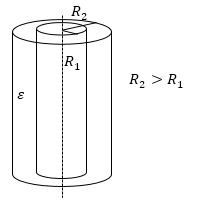
Рис. 3

Еще одной, но не маловажной характеристикой всех конденсаторов является пробивное напряжение ($U_{max}$)-- это напряжение, при котором происходит электрический разряд через слой диэлектрика. $U_{max}$ зависит от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Помимо одиночных конденсаторов применяют их соединения. Для того чтобы увеличить емкость используют параллельное соединение конденсаторов (соединение одноименными обкладками). В этом случае результирующая емкость такого соединения может быть найдена как сумма${\ С}_i$ где $С_i$ -- емкость конденсатора с номером i:

$$C=\sum\limits^N_{i=1}{С_i}\ \left(6\right).$$

Если конденсаторы соединить последовательно (обкладками с разными знаками заряда), то суммарная емкость соединения будет всегда меньше, чем минимальная емкость любого конденсатора, который входит в систему. В этом случаем для того чтобы рассчитать результирующую емкость складывают величины, обратные к емкостям отдельных конденсаторов:

$$\frac{1}{C}=\sum\limits^N_{i=1}{{\frac{1}{C_i}}_i}\left(7\right).$$