Определение, характеристики затухающих колебаний
В реальном мире любые колебания в системе, где нет источника энергии, являются затухающими. Рассмотрим реальный контур, сопротивление которого отлично от нуля. Примером простейшей системы, которую рассматривают в таком случае может служить контур включают сопротивление $(R)$, конденсатор емкостью $C$, катушку индуктивности $L$, тогда такой контур имеет вид указанный на рис.1. Колебания в таком контуре являются затухающими.
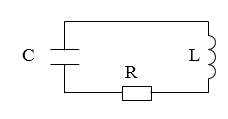
Рисунок 1.
Причиной затухания колебаний в таком контуре является наличие сопротивления. Его существование ведет к тому, что в контуре происходят потери энергии на выделение джоулева тепла. В механике аналогом сопротивления являются силы трения.
Затухающие колебания характеризуют коэффициентом затухания ($\beta $), равным:
Из выражения (1) видно, что $\beta $ является характеристикой контура. Иногда для характеристики затухания используют логарифмический декремент затухания ($\delta $), который равен:
где $a\left(t\right)$- амплитуда какой -- либо величины (заряда, силы тока и т.д.). $\delta $ равен количеству колебаний ($N_e$) за время, в течение которого амплитуда уменьшается в e раз:
Для $RLC$ контура:
где $\omega $ -- частота.
Если затухание небольшое ($\delta \ll 1$), то полагают, что $\beta \ll {\omega }_0$ (${\omega }_0=\sqrt{\frac{1}{LC}}-собственнная\ частота$), тогда $\omega \approx {\omega }_0$. В таком случае:
Рассматривая затухающие колебания, колебательный контур характеризуют его добротностью ($O$). Он равен:
Для слабого затухания добротность можно выразить как:
Также при слабом затухании электрических колебаний добротность можно выразить через отношение энергий:
где $W$ -- энергия контура, $\triangle W$- уменьшение энергии контура за одно колебание.
Уравнение затухающих колебаний
Обратимся вновь к контуру, который изображен на рис.1. Изменение заряда ($q$) на конденсаторе в таком контуре описывается дифференциальным уравнением вида:
Если сопротивление, которое входит в состав контура $R \[q(t)=A_0e^{\left(-\beta t\right)}{sin \left(\omega t+{\alpha }_0\right)=A_0e^{\left(-\beta t\right)}{cos \left(\omega t+{\alpha '}_0\right)=0\left(10\right)\ },\ }\]
где $\omega =\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}} \cdot \beta =\frac{R}{2L}$. Амплитуда равна:
В том случае, если при $t=0$ заряд на конденсаторе равен $q_0$, тока в цепи нет, то для $A_0$ можно записать:
Начальная фаза колебаний (${\alpha }_0$) равна:
При $R >2\sqrt{\frac{L}{C}}$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.
Сопротивление, при котором колебания превращаются в апериодический разряд конденсатора называется критическим ($R_k$). Величина $R_k$ определяют условием:
График функции (10) изображают как на рис.2.
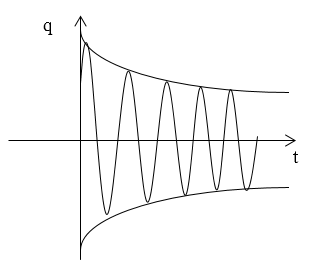
Рисунок 2.
Задание: Запишите закон убывания энергии, запасенной в контуре $(W(t))$, если $W(t=0)=W_0,$ колебания являются затухающими. Коэффициент затухания колебаний в контуре равен $\beta $. Собственная частота ${\omega }_0.\ $
Решение:
В качестве отправной точки для решения задачи используем уравнение изменения заряда на конденсаторе в $RLC$ -контуре в виде:
\[q\left(t\right)=q_0e^{\left(-\beta t\right)}{cos \left(\omega t+{{\alpha }'}_0\right)=q_0e^{\left(-\beta t\right)}cos\left(\omega t\right)\left(1.1\right)\ },\]в выражении (1.1) мы предположили, что при $t=0,\ {{\alpha }'}_0=0$. Используя выражение:
\[I=\frac{dq}{dt}\left(1.2\right).\]Найдем $I(t)$, получим:
\[I(t)=-{\omega }_0q_0e^{\left(-\beta t\right)}sin\left(\omega t+\alpha \right)\left(1.3\right),\]где $tg\alpha =\frac{\beta }{\omega }.$
Следовательно, электрическая энергия контура ($W_q$) имеет вид:
\[W_q=\frac{q^2}{2C}=\frac{{q_0}^2}{2C}e^{\left(-2\beta t\right)}cos^2\left(\omega t\right)=W_0e^{\left(-2\beta t\right)}cos^2\left(\omega t\right)\ \left(1.4\right).\]Магнитная энергия контура ($W_m$) равна:
\[W_m=\frac{L}{2}{\omega_0}^2{q_0}^2e^{\left(-2\beta t\right)}sin^2\left(\omega t+\alpha\right)=W_0e^{\left(-2\beta t\right)}sin^2\left(\omega t+\alpha\right)\left(1.5\right).\]Полная энергия равна:
\[W=W_q+W_m=W_0e^{\left(-2\beta t\right)}\left(cos^2\left(\omega t\right)+sin^2\left(\omega t+\alpha \right)\right)=W_0e^{\left(-2\beta t\right)}\left(1+\frac{\beta }{{\omega }_0}{sin \left(2\omega t+\alpha \right)\ }\right),\]где $sin\alpha =\frac{\beta}{\omega_0}.$
Ответ: $W(t)=W_0e^{\left(-2\beta t\right)}\left(1+\frac{\beta }{{\omega }_0}{sin \left(2\omega t+\alpha \right)\ }\right).$
Задание: Используя результат Примера 1, запишите выражение для энергии, запасенной в контуре ($W(t)$), если колебания затухают в контуре очень медленно. Изобразите график убывания энергии запасенной в контуре.
Решение:
Если колебания в контуре затухают медленно, то это значит:
\[\frac{\beta }{{\omega }_0}\ll 1\ \left(2.1\right).\]Следовательно, выражение для энергии, запасенной в контуре:
\[W(t)=W_0e^{\left(-2\beta t\right)}\left(1+\frac{\beta }{{\omega }_0}{sin \left(2\omega t+\alpha \right)\ }\right)(2.2)\]можно преобразовать к виду:
\[W\left(t\right)=W_0e^{\left(-2\beta t\right)}\left(2.3\right),\]так как выполняется условие (2.1), ${sin \left(2\omega t+\alpha \right)\ }\le 1,\ $значит:
\[{\frac{\beta }{{\omega }_0}sin \left(2\omega t+\alpha \right)\ll 1.\ }\]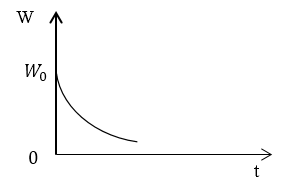
Рисунок 3.
Ответ: $W\left(t\right)=W_0e^{\left(-2\beta t\right)}$. Энергия контура убывает по экспоненте.











