Энергия магнитного поля при наличии магнетиков
Пусть все рассматриваемое пространство заполняет однородный магнетик. В нем индукция магнитного поля, которое создают токи, изменяется в $\mu $ раз в сравнении с индукцией в вакууме. Во столько же изменяются магнитные потоки $Ф$ и $dФ.$ Элементарная работа, выполняемая внешним источником против электродвижущей силы индукции, будет равна:
Допустим, что магнитное поле создается двумя контурами. Если $L_{11}$ - индуктивность первого контура, $L_{22}$ - индуктивность второго контура, то можно записать, что:
Поток ${\Phi }_{12}$, который пересекает контур (1), создаваемый током во втором контуре равен:
где $L_{12}$- постоянная, взаимная индуктивность первого и второго контуров. Для второго контура имеем:
Из формул (2) - (4) следует, что если изменяются магнитные потоки в магнетике, то индукции контура и взаимные индукции увеличиваются в $\mu $ раз. Это значит, что взаимные индукции контуров равны:
При этом магнитные потоки в магнитике могут быть выражены как:
где $r_{21}=r_{12}$ - расстояния между элементами контуров с током $d\overrightarrow{l_1}и\ d\overrightarrow{l_2}$.
Формула же записанная для энергии магнитного поля, которое создано двумя контурами с токами для вакуума и магнетика (при отсутствии ферромагнетика) по форме не изменяется:
Если магнитное поле образуется $N$ контурами, то его энергию можно вычислить как:
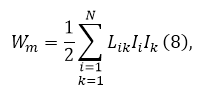
Рисунок 1.
при $i=k$ коэффициент $L_{ik}$ называется индуктивностью контура ${\rm I}$, при $i\ne k$, этот же коэффициент называют взаимной индуктивностью ${\rm I}$-го и k-го контуров. Эти коэффициенты определяются формулами при $i\ne k$:
где $d\overrightarrow{l_i},d\overrightarrow{l_k}$ - элементы длины контуров ${\rm I}$-го и $k$-го. $r_{ik}-$расстояние между ними. При этом $L_{ik}=L_{ki}$. В результате получается, что энергия магнитного поля токов, которые текут в неограниченном однородном магнетике, изменяется в $\mu $ раз в сравнении с энергией этих же токов в вакууме.
Объемная плотность энергии магнитного поля
Магнитное поле, которое создают токи, распределено по всему пространству. Допустим, что магнитное поле создается одиночным контуром с током. Магнитная энергия поля в таком случае может быть представлена как:
где поток магнитной индукции можно выразить как:
где $L$ контур тока, $S$ - поверхность, которая натянута на контур $L$, $\overrightarrow{A}\ $- векторный потенциал, магнитного поля, которое создается током $I$. Замкнутый ток взаимодействует со своим магнитным полем. Каждый элемент тока $Id\overrightarrow{l}$ создает в пространстве собственное магнитное поле, с которым взаимодействуют другие элементы тока.
Подставим (11) в формулу (10), получим:
Проведем переход от линейных токов к объемным токам с помощью соотношения:
Из выражения (10) получим:
Используем известные формулы:
Преобразуем выражение (12), получим:
По теореме Остроградского - Гаусса имеем:
В том случае, если точки рассматриваются в конечной области пространства, на больших расстояниях от этой области $A\sim \frac{1}{r}$, $H\sim \frac{1}{r^2}$, то есть подынтегральное выражение убывает пропорционально $\frac{1}{r^3}$. Поверхность при этом растет пропорционально $r^2$, получаем, что интеграл уменьшается $\sim \frac{1}{r}.$ Получается, что при $r\to \infty $, второй интеграл в выражении (15) равен нулю, тогда полная энергия выражается формулой:
Тогда, можно сказать, что объемная плотность энергии магнитного поля в пространстве равна:
Энергия магнетика во внешнем поле
Если имеется фиксированное распределение токов в пространстве, то энергия магнетика в магнитном поле равна:
где $\overrightarrow{J}$ - намагниченность магнетика, $\overrightarrow{B_0}$ - магнитное поле в свободном пространстве.
Задание: Вычислите магнитную проницаемость железа, если в поле с индукцией $B=1Тл$ плотность энергии магнитного поля в веществе $200 \frac{Дж}{м^3}$.
Решение:
В качестве основания для решения задачи используем формулу
\[w_m=\frac{1}{2}\overrightarrow{H}\overrightarrow{B}=\frac{1}{2}\frac{B^2}{\mu {\mu }_0}\ \left(1.1\right).\]Из формулы (1.1) выразим магнитную проницаемость, получим:
\[\mu =\frac{1}{2}\frac{B^2}{w_m{\mu }_0}\left(1.2\right).\]Проведем вычисления:
\[\mu =\frac{1}{2}\cdot \frac{1^2}{200\cdot 1,26\cdot {10}^{-6}}=2\cdot {10}^3.\]Ответ: $\mu =2\cdot {10}^3.$
Задание: Определите, как изменится объемная плотность энергии магнитного поля, если индукция магнитного поля тороида, который имеет ферромагнитный сердечник, увеличилась от $B_1=0,9\ Тл\ до\ B_2=1,2\ Тл$. Зависимость $B(H)$ представлена графиком на рис.2.
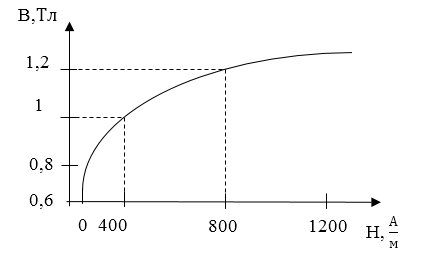
Рисунок 2.
Решение:
В качестве основания для решения задачи используем формулу
\[w_m=\frac{1}{2}\overrightarrow{H}\overrightarrow{B}\left(2.1\right).\]Запишем формулу (2.1) для двух состояний магнитного поля и найдем отношение $\frac{w_{2m}}{w_{1m}}$:
\[\frac{w_{2m}}{w_{1m}}=\frac{1}{2}H_2B_2\cdot 2\frac{1}{H_1B_1}=\frac{H_2B_2}{H_1B_1}\left(2.2\right).\]По графику находим, что при $B_1=1\ Тл\ H_1=400\frac{A}{м}\ до\ B_2=1,2\ Тл\ H_2=800\frac{A}{м}\ $.
Следовательно, искомое отношение равно:
\[\frac{w_{2m}}{w_{1m}}=\frac{1,2\cdot 800}{1\cdot 400}=2,4.\]Ответ: $\frac{w_{2m}}{w_{1m}}=2,4.\ $











