Изучение электромагнитных явлений
Началом научного изучения электрических и магнитных явлений считается работа Гильберта «О магните, магнитных телах и большом магните, новая физиология» (1600 г.), в которой он объяснил поведение стрелки компаса. Он открыл эффект усиления магнитного действия железным якорем и объяснил его намагничением железа. Гильберт ввел понятие «электричество» (это термин произведен от греческого названия янтаря). Гильберт исследовал множество различных тел с точки зрения электризации их трением. Разделил все вещества на электрические и неэлектрические. Изобрел прообраз современного электроскопа. Он разделил электрические и магнитные явления. В сочинениях Гильберта присутствует смесь интересных наблюдений, научных предположений и объяснений в стиле алхимиков. Но именно работы Гильберта дали отправную точку для интенсивного развития электромагнетизма как важнейшего раздела науки и техники.
Эклектическими опытами занимались многие ученые, состоявшие в Лондонском Королевском обществе. Ньютон рассматривал «электрическую пляску» кусочков бумаги под стеклом, положенных на металлическое кольцо, в 1716 г. получил искровой разряд между острием иглы и наэлектризованным телом. Бойль исследовал свойства притяжения наэлектризованных тел. Грэй открыл электропроводность тел, рассматривал вопросы, связанные с сохранением заряда (1730-1731 г.г.).
Чуть позже (1733 г) французский естествоиспытатель Дюфэ создал первую теорию электрических явлений. Он выделил два рода электрических взаимодействий: притяжение и отталкивание. С открытия лейденской банки началось повальное увлечение электрическими опытами в Европе, а позднее Америке и России. Крупные вклады в изучение электромагнитных явлений внесли: Рихман (электрический указатель - родоначальник современных электрометров), Франклин (теория положительного и отрицательного электричества), Кавендиш (эмпирическое доказательство того, что силы взаимодействия электрических зарядов подчиняются закону $\frac{1}{r^n},\ где\ n=2\pm \frac{1}{50}$), Кулон (закон кручения, методы измерения количества электричества и количества магнетизма, база для системы электрических и магнитных единиц), Вольта (связь между количеством электричества, емкостью и напряжением, электроскоп, первый генератор электрического тока), Эрстед (магнитное действие тока), Ампер (механическое взаимодействие токов, эмпирическая теория электродинамических явлений, создание электродинамики), Фарадей (исследования в области индукции, первая модель трансформатора), Максвелл (электромагнитная теория света, физико - математическая теория электромагнитного поля) и многие другие.
Понятие электромагнитного поля
В разделе электричество и магнетизм центральным станет понятие электромагнитного поля. Не достаточно определить, что это такое, необходимо изучить свойства этого поля. Прежде установим, чем понятие «поле» отличается от понятия «вещество». К особенностям вещества можно отнести то, что его можно разделить на независимые части -- частицы. Движение частицы характеризуют вектором скорости, ее положение описывают координаты. Следовательно, можно описывать внешнее и внутреннее состояние тела. В этом смысле поле категорически отличается от вещества. Оно заполняет все пространство, оно едино. Но в отличие от пространства поле обладает массой, энергией. Очень часто говорят о полях, но это имеется в виду разные состояния одного поля. Не говорят о перемещении поля. Поле может воздействовать на частицы. И так, поле -- особый вид материи, одним из существенных свойств которого является единство, не возможно разбить его на самостоятельно существующие части. В виду выше сказанного поле описывается по его действию на частицы вещества. В том случае, если поле на частицу действует силой, частица называется заряженной, если не действует - нейтральной.
Сила, с которой поле действует на частицу называется электромагнитной ($\overrightarrow{F}$):
\[\overrightarrow{F}={\overrightarrow{F}}_E+{\overrightarrow{F}}_M\ \left(1\right),\]где ${\overrightarrow{F}}_E$- электрическая сила (не зависит от скорости движения частицы), ${\overrightarrow{F}}_M(\overrightarrow{v})$- магнитная сила (равно нулю, если частица не движется).
Исходя из разбиения (1) поле так же принято разбивать на электрическое и магнитное, которые являются лишь особыми состояниями одного электромагнитного поля. Логика построения последовательности изучения электромагнитного поля соответствующая. В начале рассматривается электрическое поле, за тем магнитное, потом объединенное - электромагнитное.
Немаловажным является вопрос о способах создания электромагнитного поля. Частицы, обладающие электрическими зарядами, являются создателями (возбудителями) полей. Вокруг всяких заряженных частиц возникает электрическое поле, но только вокруг движущихся, возникает магнитное поле и действует оно только на движущиеся частицы. Если неподвижные частицы создают электрическое поле, что оно называется электростатическим.
Свой опыт по сравнению электрической силы Рихман описывал следующим образом: К железной проволоке CB, отводящей электричество, я подвесил льняную нитку DE, затем на расстоянии 492 лондонских линии я укрепил шелковую голубую нитку, параллельную горизонту, а в g поместил тяжелое тело. Шелковую нитку Eg я разделил на десятые доли лондонского фунта, обозначив точки деления льняными нитками. Когда проволоке сообщали электричество, нитка DE приближалась тяжелому телу g и принимала наклонное положение. Когда электричество прекращалось, нитка вновь принимала вертикальное положение DB. Да позволено будет назвать указателем электричества нить DE, свисающую с наделенной электричеством проволоки и приближающуюся к тяжелому телу. Решим задачу, приблизительно, соответствующую данному опыту.
Задание: Два одинаковых маленьких шарика с массами m подвешены на шелковых нитях длины l. Шариками сообщили одинаковые по величине и знаку заряды. Каков заряд шариков, если они разошлись так, что нити образуют угол $2\alpha ?$
Решение:
Изобразим силы, действующие на один из шариков на рис. 1. Запишем уравнение равновесия:
\[\overrightarrow{F_e}+\overrightarrow{mg}+\overrightarrow{N}=0\ \left(1.1\right).\]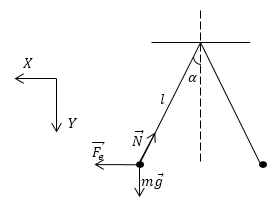
Рис. 1
Запишем проекции уравнения (1) на оси:
OX: $F_e-Nsin\alpha =0,\left(1.2\right),$ OY: $mg-Ncos\alpha =0\left(1.3\right).$Разделим (1.2) на (1.3), получим:
\[\frac{F_e}{mg}=tg\alpha \ \left(1.4\right).\]В уравнении (1.4) $F_e$- сила Кулона, выражение для которой в системе СГС будет иметь вид:
\[F_e=\frac{q_1q_2}{r^2}\ \left(1.5\right),\]где $q_{1,}q_2$ заряды шариков, r -- расстояние между шариками, которые мы в данном случае принимаем за точечные. Найдем r из прямоугольного треугольника:
\[r=lsin\alpha \ \left(1.6\right).\]Из условия задачи мы знаем, что заряды шариков одинаковы, в таком случае выражение для силы Кулона запишем как:
\[F_e=\frac{q^2}{({lsin\alpha )}^2}\left(1.7\right).\]Подставим (1.7) в (1.4), получим:
\[\frac{q^2}{({lsin\alpha )}^2}=mgtg\alpha \ \to q=lsin\alpha \sqrt{mgtg\alpha }\ \left(1.8\right).\]Ответ: заряд шариков равен $q=lsin\alpha \sqrt{mgtg\alpha }.$
Задание: По тонкому проводящему кольцу радиуса R течет ток I. Найдите магнитную индукцию $\overrightarrow{B}$ в точке А равноудаленной от всех течек кольца на расстояние r.
Решение:
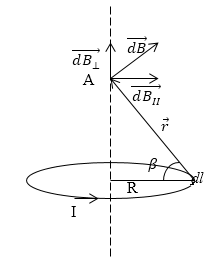
Рис. 2
В качестве основы для решения используем закон Био -- Савара -- Лапласа:
\[d\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}\ \left(2.1\right),\]где $d\overrightarrow{B}$- магнитная индукция поля, которая создается элементарным током в точке, которая определена радиус -- вектором $\overrightarrow{r}$.
Выделим на кольце элементарный участок $d\overrightarrow{l}$ и от него в точку А, которая задана в условии задачи, проведем радиус -- вектор $\overrightarrow{r}$. Вектор магнитной индукции направим по правилу буравчика. Магнитная индукция в очке А определяется как:
\[\overrightarrow{B}=\int\limits_L{d}\overrightarrow{B}\ \left(2.2\right),\]где интегрирование ведется по всем $d\overrightarrow{l}.$ Разложим вектор $\overrightarrow{B}$ на составляющую перпендикулярную плоскости кольца $d\overrightarrow{B_{\bot }}$ и параллельную плоскости кольца: $d\overrightarrow{B_{II}}$:
\[d\overrightarrow{B}=d\overrightarrow{B_{\bot }}+d\overrightarrow{B_{II}}\ \left(2.3\right).\]В таком случае (2.2) представим в виде:
\[\overrightarrow{B}=\int\limits_L{d}\overrightarrow{B_{\bot }}+\int\limits_L{d\overrightarrow{B_{II}}}\left(2.4\right),\]где
\[\int\limits_L{d\overrightarrow{B_{II}}}=0\ \left(2.5\right).\]а векторы $d\overrightarrow{B_{\bot }}$ сонаправлены следовательно, векторное суммирование можно заменить скалярным:
\[B=\int\limits_L{d\overrightarrow{B_{\bot }}\ \left(2.6\right).}\]При этом учтем, что $d\overrightarrow{B_{\bot }}=dBcos\beta $, и $dB=\frac{м_0}{4$\eth$}\frac{Idl}{r^2}$ ($d\overrightarrow{l}\bot \overrightarrow{r}$). В результате, мы получаем:
\[B=\frac{{\mu }_0}{4\pi }\frac{Icos\beta }{r^2}\int\limits^{2\pi R}_0{dl}=\frac{{\mu }_0Icos\beta }{4\pi r^2}2\pi R=\frac{{\mu }_0IR}{2r^3},\]где $cos\beta =\frac{R}{r}$.
Ответ: Магнитная индукция В=$\frac{{\mu }_0IR}{2r^3}$.











