Создание модели Вселенной
В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.
Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.
Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации - открытию закона всемирного тяготения.
С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям. Первая попытка создания модели Вселенной была предпринята Птолемеем ($140$ г.). В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.
Геоцентрическая система Птолемея продержалась более $14$ столетий и только в середине $XVI$ века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми. Немецкий астроном И.Кеплер в начале $XVII$ века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы.
Изучая результаты многолетних наблюдений планеты Марс датским астрономом Т. Браге, немецкий ученый И. Кеплер обнаружил, что орбита Марса не окружность, а имеет вытянутую форму эллипса. Как известно, у эллипса есть две точки $F_{1} $ и $F_{2} $ (рис. 1), сумма расстояний которых ($r_{1} +r_{2} $) от любой точки В эллипса есть величина постоянная.
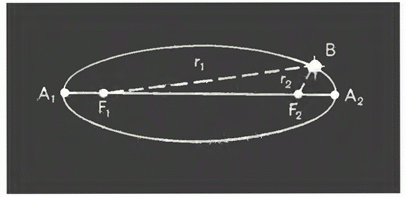
Рисунок 1.
Прямая $A_1A_2$, лежащая внутри эллипса и проходящая через его фокусы, называется большой осью эллипса. Мерой сплюснутости эллипса является его эксцентриситет, равный отношению расстояния между фокусами к большой оси $5=\frac{F_{} F_{} }{A_{1} A_{2} } $. Линия, соединяющая любую точку эллипса с одним из его фокусов, называется радиусом-вектором этой точки.
Три закона движения планет
Кеплер исследовал движения всех известных в то время планет и вывел три закона движения планет.
Во-первых, орбиты всех планет (а не только Марса) являются эллипсами с общим фокусом, в котором находится Солнце. Степень вытянутости орбит у разных планет различная. У Земли эксцентриситет очень мал (всего $0,017$), и орбита Земли мало отличается от окружности. Поэтому кратчайшее расстояние Земли от Солнца (в перигелии) мало отличается от наибольшего (в афелии). Наиболее вытянутые орбиты имеют Меркурий (эксцентриситет $0,21$) и Плутон (эксцентриситет $0,25$).
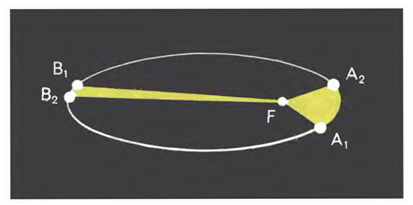
Рисунок 2.
Во-вторых, каждая планета по своей орбите движется таким образом, что ее радиус-вектор за одинаковые промежутки времени описывает равные площади (площади секторов $A_1A_2F$ и $B_1B_2F$ на рис. 2 равны). Это значит, что чем ближе планета к Солнцу, тем у нее больше скорость движения по орбите. Например, Марс вблизи перигелия движется со скоростью $26,5$ км/с, а около афелия его скорость уменьшается до $22$ км/с.
Кометы, являясь членами Солнечной системы, движутся по тем же законам, что и планеты, но у некоторых из них орбиты настолько вытянуты, что вблизи Солнца скорость их движения доходит до $500$ км/с, а в афелии их скорость снижается до $1$ см/с.
Первые два закона движения планет Солнечной системы Кеплер опубликовал в $1609$ г. Спустя десять лет он обнаружил третью закономерность в движении планет и сформулировал ее так: отношение кубов больших полуосей орбит двух любых планет Солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца.
Этот закон имел большое значение для определения масштабов Солнечной системы, т. е. расстояний планет от Солнца. Если за единицу времени принять один год, а за единицу расстояния --- среднее расстояние Земли от Солнца (астрономическую единицу), то, определив из наблюдений период обращения какой-либо планеты в годах ($T$), легко получить значение большой полуоси этой планеты ($a$) по формуле:
Например, период обращения Марса по наблюдениям равен $1,88$ года. Тогда по этой формуле можно вычислить большую полуось орбиты Марса, которая оказывается равной $1,52$ а. е. Таким образом, Марс примерно в полтора раза дальше от Солнца, чем Земля.
Установленные Кеплером законы движения планет еще раз наглядно показывают, что мир планет есть стройная система, управляемая единой силой, источником которой является Солнце.
Определите, во сколько раз масса Солнца больше массы Земли, если известно, что период обращения Луны вокруг Земли $27,2$ сут., а среднее расстояние ее от Земли $384000$ км.
Дано: $T_{;} =27,2$сут., $a_{;} =3.84\cdot 10^{5} $км.
Найти: $\frac{m_{c} }{m_{3} } $-?
Решение: $T_{3} =365$сут -- период обращения Земли вокруг Солнца
$a_{3} =1.5\cdot 10^{8} $км -- среднее расстояние от Земли до Солнца.
Для решения используем формулу третьего закона Кеплера с учетом второго закона Ньютона:
\[\frac{m_{c} +m_{3} }{m_{3} +m_{;} } \cdot \frac{T_{3}^{2} }{T_{;}^{2} } =\frac{a_{3}^{3} }{a_{;}^{3} } .\]Учитывая, что масса Земли по отношению к массе Солнца и масса Луны по отношению к массе Земли ничтожно малы, то формулу можно переписать в виде:
\[\frac{m_{c} }{m_{3} } \cdot \frac{T_{3}^{2} }{T_{;}^{2} } =\frac{a_{3}^{3} }{a_{;}^{3} } \]Отсюда находим искомое отношение масс:
\[\frac{m_{c} }{m_{3} } =\frac{a_{3}^{3} }{a_{;}^{3} } \cdot \frac{T_{3}^{2} }{T_{;}^{2} } .\]Ответ: $\frac{m_{c} }{m_{3} } =0,3\cdot 10^{6} $.











