Законы динамики в неинерциальных системах отсчета
Как известно, законы Ньютона выполняются только в инерциальных системах отсчета. Системы отсчета, которые движутся относительно инерциальной системы с ускорением, называются неинерциальными. В неинерциальных системах законы Ньютона, вообще говоря, уже применять нельзя. Однако законы динамики можно применять и для них, если кроме сил, которые обусловлены воздействием тел друг на друга, ввести в рассмотрение понятие силы особого рода - так называемую силу инерции.
При учете сил инерции второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (учитывая и силы инерции). При этом силы инерции $F_{in} $ должны быть такими, чтобы вместе с силами $F$, обусловленными воздействием тел друг на друга, они сообщали телу ускорение $a'$, каким оно обладает в неинерциальных системах отсчета, т. е. :
$ma'=F+F_{in} $ (1).
Так как $F=ma$ ($a$ - ускорение тела в инерциальной системе отсчета), то:
Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, поэтому, в общем случае, следует учитывать следующие случаи возникновения этих сил:
- силы инерции при ускоренном поступательном движении системы отсчета;
- силы инерции, которые действуют на тело, покоящееся во вращающейся системе отсчета;
- силы инерции, которые действуют на тело, движущееся во вращающейся системе отсчета.
Рассмотрим эти случаи.
Силы инерции при ускоренном поступательном движении системы отсчета
На тележке к штативу на нити подвешен шарик массой $m$ (рис. 1).
Пока тележка покоится или движется прямолинейно и равномерно, нить, которая удерживает шарик, занимает вертикальное положение и сила тяжести $P$ уравновешивается силой реакции (натяжения) нити $T$. Если тележку привести в поступательное движение с ускорением $a_{0} $, то нить будет отклоняться от вертикали в сторону, обратную движению, до такого угла $\alpha $, пока результирующая сила $F=P+T$не даст ускорение шарика, равное $a_{0} $. Значит, результирующая сила $F$ направлена в сторону ускорения тележки $a_{0} $ и для установившегося движения шарика (теперь шарик движется вместе с тележкой с ускорением $a_{0} $) равна $F=mgtg\alpha =ma_{0} $, откуда $tg\alpha =\frac{a_{0} }{g} $, т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки. В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила $F$ уравновешивается равной и противоположно направленной ей силой $F_{in} $, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют.
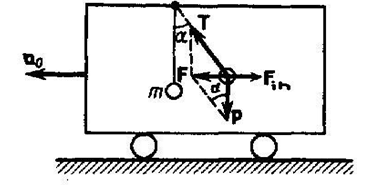
Рисунок 1.
Таким образом:
$F_{in} =-ma_{0} $. (2)
Силы инерции, действующие на тело, покоящееся во вращающейся системе отсчета
Пусть диск равномерно вращается с угловой скоростью $\omega $ ($\omega =const$) вокруг перпендикулярной ему оси, которая проходит через его центр. На диске установлены маятники, на разных расстояниях от оси вращения и на нитях висят шарики массой $m$. Когда диск начнет вращаться, шарики отклоняются от вертикали на некоторый угол (рис.2).
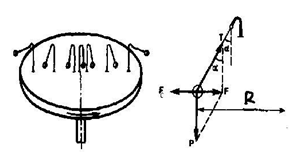
Рисунок 2.
В инерциальной системе отсчета, которая связана, например, с помещением, где установлен диск, происходит равномерное вращение шарика по окружности радиусом $R$ (расстояние от центра вращающегося шарика до оси вращения). Значит, на него действует сила, равная $F=m\omega ^{2} R$ и которая направлена перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести $\; $ и силы реакции (натяжения) нити $T$: $F=P+T$. Когда движение шарика установится, то $F=mgtg\alpha =m\omega ^{2} R$ откуда:
$tg\alpha =\frac{\omega ^{2} R}{g} $ ,
т. е. углы отклонения нитей маятников будут тем больше, чем больше угловая скорость вращения и чем больше расстояние $R$ от центра шарика до оси вращения диска. Относительно системы отсчета, которая связана с вращающимся диском, шарик покоится, что возможно, если сила $F$ уравновешивается равной и противоположно направленной ей силой $F_{c} $, являющаяся ничем иным, как силой инерции, так как никакие другие силы на шарик не действуют. Сила $F_{c} $, называемая \textbf{центробежной силой инерции}, направлена по горизонтали от оси вращения диска и равна:
$F_{c} =-ma_{0} \omega ^{2} R$. (3)
Из формулы (3) следует, что центробежная сила инерции, которая действует на тела во вращающихся системах отсчета и которая направлена в сторону радиуса от оси вращения, зависит от угловой скорости вращения $\omega $ системы отсчета и радиуса $R$, но при этом не зависит от скорости тела относительно вращающихся систем отсчета. Значит, центробежная сила инерции действует во вращающихся системах отсчета на все тела, которые удалены от оси вращения на конечное расстояние, при этом не имеет значения, покоятся ли они в этой системе отсчета (как мы предполагали до сих пор) или движутся относительно нее с некоторой скоростью.
Силы инерции, действующие на тело, движущееся во вращающейся системе отсчета
Пусть шарик массой $m$ движется с постоянной скоростью $v'$ вдоль радиуса равномерно вращающегося диска ($v'=const$,$\omega =const$,$v'$ перпендикулярно $\omega $). Если диск не начал вращаться, то шарик, движется по радиальной прямой и попадает в точку А, если же диск привести во вращение в направлении, которое указанно стрелкой, то шарик покатится по кривой OВ (рис. 3а), причем его скорость $v'$ относительно диска сменит свое направление. Это возможно лишь в случае, если на шарик действует сила, которая перпендикулярна скорости $v'$.
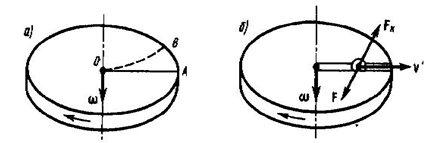
Рисунок 3.
Чтобы заставить шарик катиться по вращающемуся диску вдоль радиуса, будем использовать жестко укрепленный вдоль радиуса диска стержень, на котором шарик движется без трения прямолинейно равномерно со скоростью $v'$ (рис. 3б). При отклонении шарика стержень действует на него с некоторой силой $F$. Во вращающейся системы отсчета, т.е. относительно диска, шарик движется прямолинейно и раномерно, что объясняется тем, что сила $F$ уравновешивается приложенной к шарику силой инерции $F_{k} $, которая перпендикулярной скорости $v'$. Эта сила называется \textbf{кориолисовой силой инерции}. Можно показать, что сила Кориолиса:
Вектор $F_{k} $ перпендикулярен векторам скорости $v'$ тела и угловой скорости вращения системы отсчета в соответствии с правилом правого винта.
Тело находится в покое на вершине наклонной плоскости. За какое время тело соскользнет с плоскости, если плоскость в момент времени $е=0$ начнет двигаться влево в горизонтальном направлении с ускорением $1 \ м/с^2$? Длина плоскости $1$ м, угол наклона плоскости к горизонту $30^\circ$, коэффициент трения между телом и плоскостью $0,6$.
Найти: время движения тела по наклонной плоскости.
Решение: Систему отсчета удобно связать с наклонной плоскостью. Но плоскость движется с ускорением по отношению к Земле. Для рассматриваемого движения Земля является инерциальной системой отсчета. Следовательно, система отсчета, связанная с наклонной плоскостью, неинерциальна, и в уравнении движения тела необходимо ввести поступательную силу инерции. Таким образом, на движущееся тело в системе отсчета, связанной с наклонной плоскостью, действуют четыре силы: сила тяжести $mg$, сила нормальной реакции $N$, сила трения $F_{mp} $ и поступательная сила инерции $\overline{F}_{in} =-m\overline{a}$.
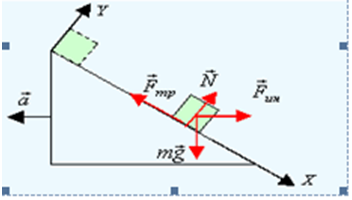
Рисунок 4.
Уравнение движения тела запишется следующим образом:
$m\overline{a_{1} }=m\overline{g}+\overline{N}+\overline{F}_{mp} +\overline{F}_{in} $ ,
где инерции $\overline{a_{1} }$ -- ускорение тела.
Спроецируем это уравнение на ось $X$, направленную вдоль наклонной плоскости, и перпендикулярную к ней ось $Y$.
\[ma_{1} =mg\sin \alpha -F_{mp} +ma\cos \alpha \] \[0=-mg\cos \alpha +N+ma\sin \alpha \]Учитывая, что $F_{mp} =\mu N$, из этой системы уравнений получим:
\[a_{1} =g(\sin \alpha -\mu \cos \alpha )+a(\cos \alpha +\mu \sin \alpha ).\]Так как ускорение $a_{1} $ не зависит от времени, то время движения тела по наклонной плоскости будет равно:
$t=\sqrt{\frac{2l}{a_{1} } } =\sqrt{\frac{2l}{g(\sin \alpha -\mu \cos \alpha )+a(\cos \alpha +\mu \sin \alpha )} } \approx 0,8$с
Ответ: $t=0,8$с.











