Ускорение тела, возникающее вследствие силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ - тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.
Под действием сила трения $\overline{F}_{mp} $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.

Рисунок 1.
Так как сила трения $\overline{F}_{mp} $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $\left|\overline{F}_{mp} \right|$, то:
Но ускорение определяется также формулой:
где $v_{0} $- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
Таким образом:
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Так как $v=0$, то:
Так как $\overline{a}=-\frac{\left|\overline{F}_{mp} \right|}{m} $, получим:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $\mu =0,25$.
Найти: $v$-?
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
$l=\frac{mv_{0}^{2} }{2\overline{\left|F_{mp} \right|}} $. (1)
Так как $F_{mp} =\mu mg$, подставим в формулу (1) и получим:
$l=\frac{mv_{0}^{2} }{2\mu mg} $. (2)
Выразив из формулы (2) $v_{0} $найдем величину искомой скорости:
$v_{0} =\sqrt{2\mu gl} =20$м/с
Ответ: Скорость автомобиля до выключения двигателя $v_{0} =20$ м/с.
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_{0} =20$м/с, $t=40$с.
Найти: $F_{mp} $, $\mu $-?
Решение:
Уравнение движения сноубордиста будет иметь вид:
\[ma=F_{mp} .\]Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
\[a=-\frac{v_{0} }{t} .\]Тогда:
$F_{mp} =ma=-m\frac{v_{0} }{t} =40H$.
Так как сила трения $\overline{F}_{mp} $равна $F_{mp} =\mu Bg$, находим коэффициент трения $\mu $:
\[\mu =\frac{F_{mp} }{mg} =0,05.\]Ответ: $F_{mp} =40H$, $\mu =0,05$.
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^\circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $\alpha =30^\circ$, $\mu =0,5$.
Найти: $a$-?
Решение:
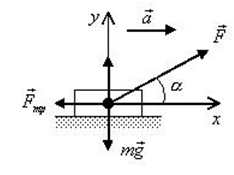
Рисунок 2.
Уравнение движения тела:
\[m\overline{a}=m\overline{g}+\overline{N}+\overline{F}+\overline{F}_{mp} .\]Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
\[\begin{array}{l} {ma=F\cos \alpha -F_{mp} } \\ {0=-Bg+N+F\sin \alpha } \end{array}\]Поскольку $F_{mp} =\mu N$, а из второго уравнения $N=mg-F\sin \alpha $, то $F_{mp} =\mu (mg-F\sin \alpha )$. Тогда из первого уравнения ускорение:
$a=\frac{1}{m} [F\cos \alpha -\mu (mg-F\sin \alpha )]\approx 7,6м/с^2$
Ответ: $a$=$7,6м/с^2$












