Принципиальным различием между реляционной алгеброй и реляционным исчислением является то, что в реляционной алгебре получение искомого результата описывается явным образом с помощью указания набора операций, которые необходимо выполнить для получения результата, а в реляционном исчислении указывают свойства искомого отношения без указания процедуры его получения.
Алгоритм редукции Кодда
Рассмотрим возможность формулировки одного и того же запроса языком реляционной алгебры и реляционного исчисления.
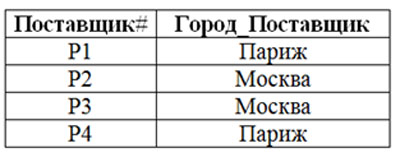
Рассмотрим запрос: «Получить города и номера поставщиков, которые выпускают деталь D2».
Словесно языком реляционной алгебры запрос может быть описан следующим образом:
- выполнить соединение отношений P и PD по атрибуту Поставщик#;
- выбрать из полученного соединения кортежи с деталью D2 (поле Деталь# должно содержать строку D2);
- выполнить проекцию результата на атрибуты Поставщик# и ГородПоставщик.
С помощью реляционного исчисления данный запрос может быть сформулирован следующим образом:
«Получить атрибуты Поставщик# и Город_Поставщик для тех поставщиков, которые имеют поставку в отношении PD с таким же значением атрибута Поставщик# и со значением D" атрибута Деталь#».
Отношение R будет результатом выполнения данного запроса:
Преимущество реляционного исчисления перед реляционной алгеброй состоит в том, что пользователь не должен сам строить алгоритм выполнения запроса. Эффективный алгоритм строится программой СУБД.
Исчисление предикатов, раздел математической логики, является математической основой реляционного исчисления.
Впервые понятие реляционного исчисления для работы с базами данных предложил Кодд. Он разработал язык ALPHA, который стал прототипом программно реализованного языка QUEL, который одно время конкурировал с языком SQL.
Исчисления существуют в двух вариантах:
- Исчисление кортежей – для описания отношений используют переменные, которые в качестве допустимых значений содержат кортежи отношения.
- Исчисление доменов – для описания отношений используют переменные, которые в качестве допустимых значений содержат элементы домена.
Исчисление кортежей
Реляционное исчисление кортежей было реализовано при разработке языка ALPHA. Как и в процедурных языках программирования, в нем сначала необходимо выполнить описание используемых переменных, а после записать выражения.
Описывается исчисление следующим образом:
RANGE OF IS ,
где RANGE, OF, IS – ключевые слова языка,
– переменная кортежа,
— последовательность из одного или большего количества элементов, записанных через запятые, т.е. в виде $х1, х2, х3, \cdots, хn, \cdots$ .
Конструкцией RANGE указывается идентификатор переменной и область допустимых значений переменной. Элементы $х1, х2, х3, \cdots, хn, \cdots$ являются отношением или выражением над отношения. Элементы списка должны быть совместимыми по типу. Областью допустимых значений переменной является объединение значений всех элементов списка.
Например, запись RANGE OF A IS A1, A2 значит, что область определения переменной А содержит все значения из отношения, являющегося объединением отношений А1 и А2.
Исчисление доменов
Реляционное исчисление, основанное на доменах, было предложено Лакроиксом и Пиротте, которыми также был разработан на его основе язык ILL.
Среди языков, основанных на исчислении доменов, можно выделить QBE с некоторыми оговорками, DEDUCE и FQL.
Дейт утверждал, что язык QBE содержит элементы исчисления кортежей и доменов, но является более близким к исчислению доменов. Языком не поддерживается операция отрицания квантора существования (NOT EXISTS), поэтому его нельзя назвать реляционно полным. Тем не менее, язык QBE достаточно широко распространен в современных СУБД.
Исчисление доменов сходно с исчислением кортежей. Основой любого выражения запроса в исчислении доменов являются переменные доменов.
Переменной домена является скалярная переменная, которая в качестве значений содержит элементы какого-нибудь домена.
Основное различие исчисления кортежей и исчисления доменов состоит в том, что исчислением доменов поддерживается дополнительная форма условия, которая называется условием принадлежности.
Общий вид условия принадлежности:
$R(A1:\vartheta_1, A2: \vartheta_2, \cdots)$,
где $Аi$ – атрибут отношения $R$, а $\vartheta_i$ – переменная домена или литерал. Проверяемое условие истинно, если и только если существует кортеж в отношении $R$, имеющий атрибуты $А$, равные заданным в выражении соответствующим значениям $\vartheta$.
Например, выражение PD (Поставщик# : ‘P1’, Деталь# : ‘D1’) будет истинным в случае, когда в отношении PD существует хотя бы один кортеж, который содержит значение ‘P1’ атрибута Поставщик# и значением ‘D1’ атрибута Деталь#.