Языки запросов на основе реляционной алгебры не получили широкого распространения в современных СУБД. Знание реляционной алгебры необходимо для того, чтобы понять суть реляционных операций, которые используют другие языки.
Коддом был предложен вариант реляционной алгебры, который содержит основные операции объединения, разности (вычитания), пересечения, декартова (прямого) произведения (или просто произведения), выборки (селекции, ограничения), проекции, деления и соединения.
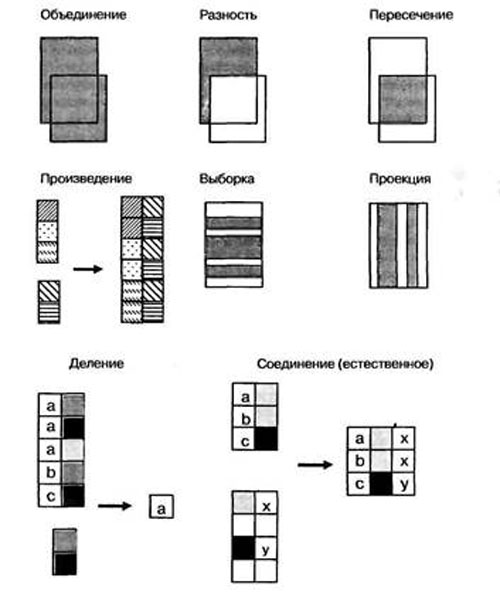
На рисунке 1 представлено графическое представление названных операций.
Недостатки реляционной алгебры Кодда
Реляционная алгебра, предложенная Коддом, имеет несколько недостатков:
- Перечисленные операции являются избыточными, т.к. минимально необходимым набором являются 5 операций: операция объединения, вычитания, произведения, проекции и выборки. Остальные 3 операции (пересечения, соединения и деления) можно представить в виде комбинации пяти минимально необходимых. К примеру, соединение является проекцией выборки произведения.
- Названных операций недостаточно для возможности построения реальной системы построения БД, основанной на принципах реляционной алгебры. Необходимы расширения, которые включают операции переименования атрибутов, создания новых вычисляемых атрибутов, нахождения итоговых функций, составления сложных алгебраических выражений, сравнения, присвоения и т.д.
Операции реляционной алгебры Кодда
Операции реляционной алгебры Кодда делятся на 2 группы:
- Базовые теоретико-множественные – включают классические операции теории множеств: объединения, разности, пересечения и произведения.
- Специальные реляционные – включают операции проекции, селекции, деления и соединения.
Операции реляционной алгебры могут быть унарными – выполненными над одним отношением (к примеру, проекция), и бинарными – выполненными над двумя отношениями (к примеру, разность).
Отношения, над которыми выполняется бинарная операция, должны быть совместимыми по структуре.
Под совместимостью структур отношений понимается совместимость типов соответствующих доменов и имен атрибутов.
Частный случай совместимости – совпадение (идентичность).
Объединение
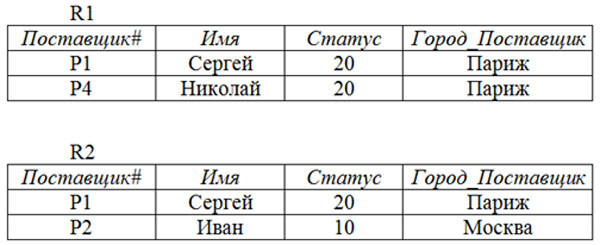
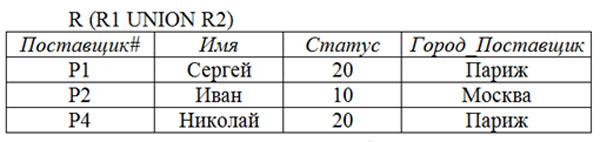
Отношение $R$ является объединением ($R1 UNION R2$) двух совместимых отношений одинаковой размерности $R1$ и $R2$, если оно содержит все элементы исходных отношений, исключая повторения.
Пусть отношение $R1$ является множеством поставщиков из Парижа, а отношение $R2$ – множеством поставщиков, выпускающих деталь $D1$. Тогда отношением $R$ будут поставщики, которые находятся в Париже, поставщики, которые выпускают деталь $D1$, или те и другие.
Вычитание
Отношение $R$ является вычитанием ($R1 MINUS R2$) совместимых отношений одинаковой размерности $R1$ и $R2$, если оно содержит множество кортежей, которые принадлежат $R1$, но не принадлежат отношению $R2$.
Для отношений $R1$ и $R2$ из рассмотренного примера отношение $R$ будет являться множеством поставщиков, которые находятся в Париже, но не выпускают деталь $D1$, то есть $R={(D4, Николай, 20, Париж)}$.
Обратим внимание, что выполнение вычитания зависит от порядка следования операндов, то есть результаты выполнения операций $R2 MINUS R1$ и $R1 MINUS R2$ будут разными.
Пересечение
Отношение $R$ является пересечением ($R1 INTERSECT R2$) двух совместимых отношений одинаковой размерности $R1$ и $R2$, если оно содержит кортежи, которые одновременно принадлежат обоим исходным отношениям.
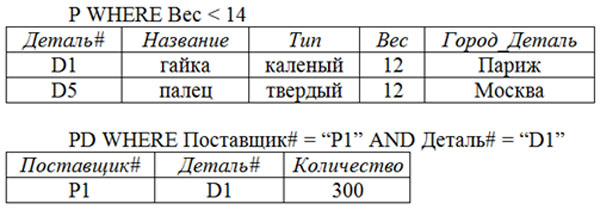
Отношение $R$ для отношений $R1$ и $R2$ будет состоять из всех производителей из Парижа, которые выпускают деталь $D1$. Таким образом, отношение $R$ содержит единственный элемент $(D1, Сергей, 20, Париж)$.
Произведение
Произведением ($R1 TIMES R2$) отношения $R1$ степени $s1$ и отношения $R2$ степени $s2$, которые не содержат одинаковые имена атрибутов, является такое отношение $R$ степени $(s1+s2)$, которое имеет заголовок в виде сцепления заголовков отношений $R1$ и $R2$ и содержит кортежи, первые $s1$ элементов кортежей из которых принадлежат множеству $R1$, а следующие $s2$ элементов принадлежат множеству $R2$.
Пусть отношение $R1$ является множеством номеров всех поставщиков ${P1, P2, P3, P4, P5}$, а отношение $R2$ – множеством номеров всех деталей ${D1, D2, D3, D4, D5, D6}$. Результат операции $R1 TIMES R2$ является множеством всех пар типа «поставщик – деталь», т.е. ${(P1,D1), (P1,D2), (P1,D3), (P1,D4), (P1,D5), (P1,D6), (P2,D1), \cdots, (P5,D6)}$.
Выборка
Выборкой ($R WHERE f$) отношения $R$ по формуле $f$ является новое отношение, которое имеет такой же заголовок, и тело, состоящее из кортежей отношения $R$, удовлетворяющих истинности логического выражения, которое задано формулой $f$.
При записи формулы используют операнды – имена атрибутов (можно номера столбцов), логические операции (NOT – НЕ, OR – ИЛИ, AND – И), константы, скобки и операции сравнения.
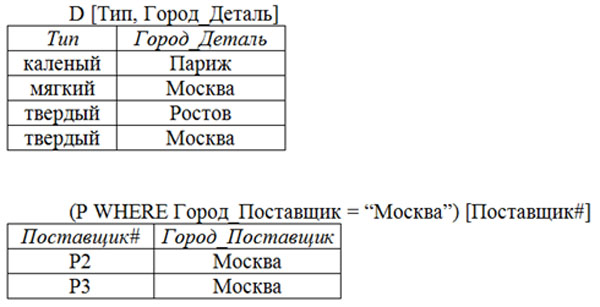
Проекция
Проекцией отношения $R$ на атрибуты $А, В, С, \cdots (R [А, В, С, \cdots])$, где множество ${А, В, С, \cdots}$ – подмножество полного списка атрибутов заголовка отношения $R$, является отношение с заголовком $А, В, С, \cdots$ и телом, которое содержит кортежи отношения $R$ без повторяющихся кортежей.
Наличие одинаковых атрибутов в списке $А, В, С, \cdots$ недопустимо.
Деление
Отношение $R$ является делением ($R1 DIVIDEBY R2$) отношения $R1$ с атрибутами $А$ и $В$ на отношение $R2$ с атрибутом $В$ ($А$ и $В$ могут быть простыми или составными атрибутами, $В$ – общий атрибут, который определен на одном и том же домене), если оно имеет заголовок $А$ и тело, состоящее из кортежей $r$ таких, что отношение $R1$ содержит кортежи $(r, s)$, к тому же множество значений $s$ содержит множество значений атрибута $В$ отношения $R2$.
Соединение
Отношение $R$ является соединением $Cf(R1, R2)$ отношений $R1$ и $R2$ по заданному формулой $f$ условию, если его можно получить с помощью декартова произведения отношений $R1$ и $R2$ с применением к полученному результату операции выборки по формуле $f$.
Иначе говоря, соединение отношения $R1$ по атрибуту $Х$ с отношением $R2$ по атрибуту $Y$ (отношения не могут иметь общие имена атрибутов) является результатом выполнения операции вида:
$(R1 TIMES R2) WHERE X Q Y$,
где $Q$ является логическим выражением над атрибутами, которые определены на одном (в случае составного атрибута – на нескольких) домене. Дейтом были предложены дополнительные операции реляционной алгебры, к которым относятся: переименование, расширение, подведение итогов, присвоение, вставка, обновление, удаление, сравнение.