Основные понятия
В качестве одной из важнейших характеристик есть средние величины. В математической статистике различают несколько видов средних величин: арифметическую, геометрическую, гармоничную, квадратичную, кубичную и другие. Все перечисленные типы средних могут быть вычислены для случаев, когда каждая из вариантов вариационного ряда встречается только один раз. Когда значения варианта повторяются разное количество раз, то вычисление средних величин называются свешенными.
Для характеристики вариационного ряда один из перечисленных типов средних выбирается не произвольно, а в зависимости от особенностей явлений, что изучается и целей, для которых среднее вычисляется.
Если варианты $x_1,\ x_2,\ \dots x_n$ встречаются один раз, либо одинаковое количество раз, то степенная средняя вычисляется за формулой:
$m-$ показатель степени, что определяет тип средней.
Если варианты $x_1,\ x_2,\ \dots x_n$ встречаются разное количество раз, то степенная средняя вычисляется за формулой:
При $m=1,\ $ из формулы (1) получим невзвешенное среднее арифметическое (простое):
А из формулы (2) при $m=1$ получим взвешенное среднее арифметическое:
За данными про количество деталей, которые изготовили работники за смену вычислить среднее арифметической.
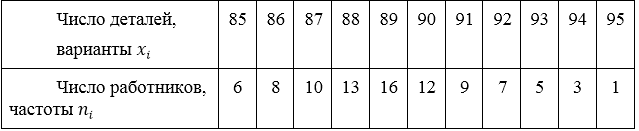
Вычислить среднее арифметическое.
\[\overline{x_в}=\frac{85\cdot 6+86\cdot 8+87\cdot 10+88\cdot 13+89\cdot 16+90\cdot 12+91\cdot 9+92\cdot 7+93\cdot 5+94\cdot 3+95\cdot 1=}{6+8+10+13+16+12+9+7+5+3+1}\] \[=\frac{510+688+870+1144+1424+1080+819+644+465+282+95}{90}=\] \[=\frac{8021}{90}\approx 89,12\ деталей.\]Мода и размах
Кроме средних в статистике для описательной характеристики величины варьирующего признака пользуются показателями моды и размаха.
Модой $M_{0} $ выборки значений случайной величины называется та варианта, которая наиболее часто встречается в выборке.
Мода применяют, к примеру при определении размера обуви, одежды, пользующейся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар и пр.
Модой в дискретном ряде называется варианта, которая имеет самую большую частоту (то есть повторяется наибольшое количество раз), например: имеем итоговую таблицу о продажах в магазине обуви по размерам:

В данном примере модой является 38-й размер, так как пар обуви данного размера продано больше всего, а именно 197 пар.
Пускай имеем интервальный ряд, то для того что б определить моду надо для начала найти модальный интервал, к тому же, если интервалы равны, то модальный интервал определяется по наибольшей частоте (если неравны -- по наибольшей плотности).
При равных интервалах моду внутри модального интервала можно определить за формулой:
\[M_0=x_0+h\frac{f_m-f_{m-1}}{\left(f_m-f_{m-1}\right)+\left(f_m+f_{m+1}\right)}\]где $x_0$ - нижняя граница модального интервала;
$h$ - величина (ширина) интервала;
$f_m$ - частота модального интервала;
$f_{m-1}$ - частота интервала, которая предшествует модальному;
$f_{m+1}$ - частота интервала, которая является следующей за модальным.
Про моду можно сказать, что она является наиболее распространенной типичной величиной в распределении. К тому же, и мода и средняя величина характеризуют совокупность по разному, а именно мода определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Поэтому мода уступает средней по своему обобщающему значению, которая характеризует совокупность в целом, так как складывается под воздействием всех без исключения элементов совокупности.
Мод может быть и несколько. Если мода одна, то распределение называется унимодальным, если две - бимодальным, при трех и более модах - мультимодальным.
Размах ряда чисел -- это разность между наибольшим и наименьшим числом в ряде.
Размах вариации одна из простейших мер колеблемости значений признака и являет собой разность между максимальным и минимальным значением признака:
\[R=X_{max}-X_{min}\]Недостатком размаха вариации является, то, что при вычислении R используется только крайние значения ряда распределения, и он не всегда правильно характеризует колеблемость данного признака.
Имея ввиду то, что каждое из индивидуальных значений признака имеет отклонения от средней на некоторую величину, то мерой вариации может выступать средняя из отклонений каждой отдельной варианты от их средней.
Такими показателями является как среднее линейное отклонение так и среднее квадратическое отклонение и дисперсия.
За данным статистическим распределением определить размах.

Размах определяется за формулой: $R=X_{max}-X_{min}=11,5-3,5=8.$











