Предварительные сведения
Неравенство вида $f(x) >( ≥)g(x)$, в котором $f(x)$ и $g(x)$ будут являться целыми рациональными выражениями, называется целым рациональным неравенством.
Примерами целых рациональных неравенств являются линейные, квадратные, кубические неравенства с двумя переменными.
Значение $x$, при котором выполняется неравенство из определения $1$, называется корнем уравнения.
Пример решения таких неравенств:
Решить целое неравенство $4x+3 >38-x$.
Решение.
Упростим данное неравенство:
$4x+x >38-3$
$5x >35$
Получили линейное неравенство. Найдем его решение:
$x >7$
Ответ: $(7,∞)$.
В данной статье мы рассмотрим следующие способы решения целых рациональных неравенств.
Способ разложения на множители
Данный способ будет заключаться в следующем: Записывается уравнение вида $f(x)=g(x)$. Данное уравнение приводится к виду $φ(x)=0$ (где $φ(x)=f(x)-g(x)$). Затем функция $φ(x)$ раскладывается на множители с минимально возможными степенями. Применяется правило: Произведение многочленов равняется нулю, когда один из них равняется нулю. Далее найденные корни отмечаются на числовой прямой и строится кривая знаков. В зависимости от знака начального неравенства записывается ответ.
Приведем примеры решения этим способом:
Решить разложением на множители. $y^2-9
Решение.
Решим уравнение $y^2-9
Используя формулу разности квадратов, имеем
$(y-3)(y+3)=0$
Используя правило равенства нулю произведения множителей, получим следующие корни: $3$ и $-3$.
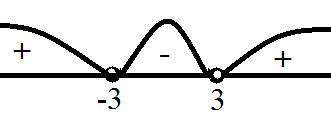
Изобразим кривую знаков:
Так как в начальном неравенстве знак «меньше», то получаем
Ответ: $(-3,3)$.
Решить разложением на множители.
$x^3+3x+2x^2+6 ≥0$
Решение.
Решим следующее уравнение:
$x^3+3x+2x^2+6=0$
Вынесем за скобки общие множители из первых двух слагаемым и из последних двух
$x(x^2+3)+2(x^2+3)=0$
Вынесем общий множитель $(x^2+3)$
$(x^2+3)(x+2)=0$
Используя правило равенства нулю произведения множителей, получим:
$x+2=0 \ и \ x^2+3=0$
$x=-2$ и "корней нет"
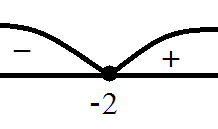
Изобразим кривую знаков:
Так как в начальном неравенстве знак «больше или равно», то получаем
Ответ: $(-∞,-2]$.
Способ введения новой переменной
Такой способ состоит в следующем: Записывается уравнение вида $f(x)=g(x)$. Решаем его следующим образом: введем такую новую переменную, чтобы получить уравнение, способ решения которого уже известен. Его, впоследствии, решаем и возвращаемся к замене. Из нее и найдем решение первого уравнения. Далее найденные корни отмечаются на числовой прямой и строится кривая знаков. В зависимости от знака начального неравенства записывается ответ.
Приведем пример применения этого способа на примере неравенства четвертой степени:
Решим неравенство.
$x^4+4x^2-21 >0$
Решение.
Решим уравнение:
$x^4+4x^2-21=0$
Сделаем следующую замену:
Пусть $x^2=u (где \ u >0)$, получаем:
$u^2+4u-21=0$
Будем решать эту систему с помощью дискриминанта:
$D=16+84=100=10^2$
Уравнение имеет два корня:
$x=\frac{-4-10}{2}=-7$ и $x=\frac{-4+10}{2}=3$
Вернемся к замене:
$x^2=-7$ и $x^2=3$
Первое уравнение не имеет решений, а из второго $x=\sqrt{3}$ и $x=-\sqrt{3}$
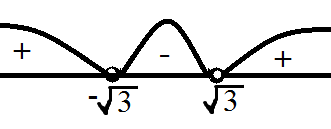
Изобразим кривую знаков:
Так как в начальном неравенстве знак «больше», то получаем
Ответ: $(-∞,-\sqrt{3})∪(\sqrt{3},∞)$