Модуль числа
Модуль числа а обозначают $|a|$. Вертикальные черточки справа и слева от числа образуют знак модуля.
Например, модуль любого числа (натурального, целого, рационального или иррационального) записывается так: $|5|$, $|-11|$, $|2,345|$, $|\sqrt[4]{45}|$.
Модуль числа a равен самому числу $a$, если $a$ является положительным, числу $−a$, если $a$ является отрицательным, или $0$, если $a=0$.
Данное определение модуля числа можно записать следующим образом:
$|a|= \begin{cases} a, & a > 0, \\ 0, & a=0,\\ -a, &a
Можно использовать более краткую запись:
$|a|=\begin{cases} a, & a \geq 0 \\ -a, & a
Вычислить модуль чисел $23$ и $-3,45$.
Решение.
Найдем модуль числа $23$.
Число $23$ – положительное, следовательно, по определению модуль положительного числа равен этому числу:
$|23|=23$.
Найдем модуль числа $–3,45$.
Число $–3,45$ – отрицательное число, следовательно согласно определению модуль отрицательного числа равен числу, противоположному данному:
$|-3,45|=3,45$.
Ответ: $|23|=23$, $|-3,45|=3,45$.
Модуль числа является абсолютной величиной числа.
Таким образом, модуль числа – число под знаком модуля без учета его знака.
Модуль числа как расстояние
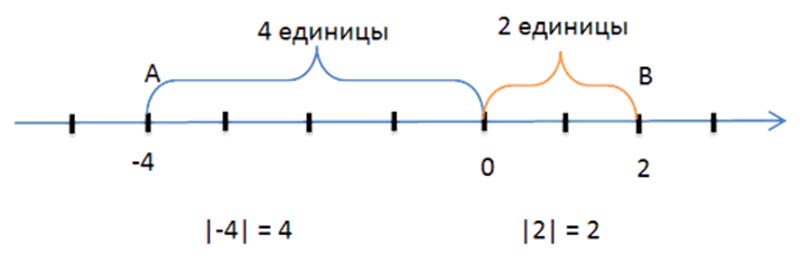
Геометрическое значение модуля числа: модуль числа – это расстояние.
Модуль числа a – это расстояние от точки отсчета (нуля) на числовой прямой до точки, которая соответствует числу $a$.
Например, модуль числа $12$ равен $12$, т.к. расстояние от точки отсчета до точки с координатой $12$ равно двенадцати:
$|12|=12$.
Точка с координатой $−8,46$ расположена от начала отсчета на расстоянии $8,46$, поэтому $|-8,46|=8,46$.
Модуль числа как арифметический квадратный корень
Модуль числа a является арифметическим квадратным корнем из $a^2$:
$|a|=\sqrt{a^2}$.
Вычислить модуль числа $–14$ с помощью определения модуля числа через квадратный корень.
Решение.
$|-14|=\sqrt{((-14)^2}=\sqrt{(-14) \cdot (-14)}=\sqrt{14 \cdot 14}=\sqrt{(14)^2}=14$.
Ответ: $|-14|=14$.
Сравнение отрицательных чисел
Сравнение отрицательных чисел основывается на сравнении модулей этих чисел.
Правило сравнения отрицательных чисел:
- Если модуль одного из отрицательных чисел больше, то такое число является меньшим;
- если модуль одного из отрицательных чисел меньше, то такое число является большим;
- если модули чисел равны, то отрицательные числа равны.
На числовой прямой меньшее отрицательное число располагается левее большего отрицательного числа.
Сравнить отрицательные числа $−27$ и $−4$.
Решение.
Согласно правилу сравнения отрицательных чисел найдем сначала модули чисел $–27$ и $–4$, а затем сравним полученные положительные числа.
$|-27|=27$
$|-4|=4$
Сравним полученные натуральные числа:
$27 > 4$.
Таким образом, получаем, что $–27 |-4|$.
Ответ: $–27
При сравнении отрицательных рациональных чисел необходимо преобразовать оба числа к виду обыкновенных дробей или десятичных дробей.
Сравнение чисел с противоположными знаками
Правило сравнения чисел с противоположными знаками:
Положительное число всегда больше отрицательного, а отрицательное число всегда меньше положительного.
Сравнить целые числа $−53$ и $8$.
Решение.
Числа имеют противоположные знаки. Согласно правилу сравнения чисел с противоположными знаками получаем, что отрицательное число $−53$ меньше положительного числа $8$.
Ответ: $−53
Сравнить числа $3 \frac{11}{13}$ и $–5,(123)$.
Решение.
Согласно правилу сравнения чисел с противоположными знаками отрицательное число всегда меньше положительного. Следовательно, $–5,(123)
Ответ: $–5,(123)
По данному правилу можно сравнивать также и действительные числа с противоположными знаками.
Если числа заданы как числовые выражения, то сразу невозможно определить какие они имеют знаки. В таком случае нужно вычислить значение этих выражений и затем определить, какое из правил сравнения можно применить.