Зависимые и независимые величины
Одним из основных инструментов для описания окружающего нас мира являются величины.
Величина – это такое свойство предмета или объекта, которое можно измерить.
Например, рост человека, высота столба, ширина забора, скорость полета.
Величины могут быть связанными между собой, зависимыми или независимыми одна от другой.
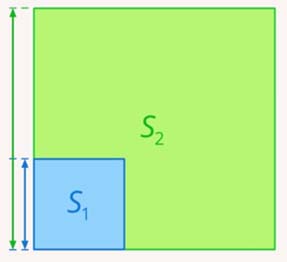
Например, длина стороны квадрата связана с площадью квадрата. При изменении длины стороны квадрата изменится и его площадь.
Рассмотрим еще один пример. Ученик идет в школу с некоторой скоростью (первая величина). В портфеле у него находится некоторое количество учебников (вторая величина).
При изменении скорости движения (первой величины) учеником количество учебников (второй величины) при этом не изменится. Следовательно, величины являются независимыми.
Иногда непосредственно повлиять на нужную величину невозможно. Тогда для изменения такой величины необходимо повлиять на промежуточную величину, от которой она зависит.
В таких случаях необходимо понимать связь между величинами, то, как при изменении одной величины изменится другая величина.
Описание изменения величины
Описание изменения температуры.
В полдень наблюдалось изменение температуры на $+6$ градусов, а к вечеру температура изменилась на $–4$ градуса.
Уменьшение величины выражается с помощью отрицательных чисел, а увеличение – с помощью положительных чисел.
Описание изменения количества денег на счете телефона.
На счету мобильного телефона было $50$ рублей. На второй день количество денежных средств изменилось на $–14$ рублей. Число $–14$ – отрицательное, что указывает на уменьшение количества денег, которые были потрачены, например, на смс-сообщения, выход в Интернет и звонки. Остаток на счете составил $36$ рублей. За третий день количество денег изменилось на $–8$ рублей, а значит, уменьшилось, т.к. $–8$ – отрицательное число. На счету осталось $28$ руб. На четвертый день счет был пополнен на $20$ руб., т.е. количество денег увеличилось, т.к. число $20$ – положительное. Остаток на счете составил $48$ рублей.
Пример.
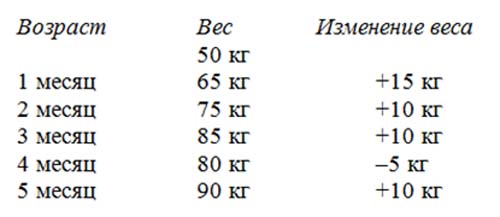
Описание изменения веса тигренка.
При рождении тигренок весил $50$ кг. За первый месяц его вес изменился на $+15$ кг, т.е. увеличился. За $2$-й и $3$-й месяц вес изменялся на $10$ кг. За $4$-й месяц вес тигренка изменился на $–5$ кг, т.е. уменьшился. Возможно, тигренок болел. В следующем месяце тигренок снова поправился на $10$ кг.
Изменение координаты точки на прямой
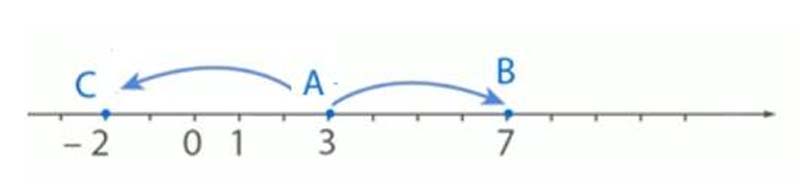
При перемещении точки по координатной прямой ее координата будет изменяться. Причем при перемещении вправо изменение координаты (увеличение) описывается положительным числом, а при перемещении влево (уменьшении) – отрицательным числом.
Например, при перемещении точки $A$ в точку $B$ изменение координаты составляет $+4$ единицы. При перемещении точки $A$ в точку $C$ координата изменится на $–5$ единиц.
Найти изменение координаты точки при ее перемещении по координатной прямой:
- от $A$ до $B$;
- от $B$ до $A$;
- от $A$ до $C$;
- от $B$ до $C$;
- от $C$ до $K$.
Решение.
- Перемещение от $A$ до $B$. Точка сдвинулась вправо на $3$ единицы, следовательно, перемещение равно $+3$ (или просто $3$).
- Перемещение от $B$ до $A$. Точка сдвинулась влево на 3 единицы, следовательно, перемещение равно $–3$ единицы.
- Перемещение от $A$ до $C$. Точка сдвинулась влево, т.е. перемещение будет отрицательным числом и составит $–7$ единиц.
- Перемещение точки $B$ в точку $C$ равно $–10$ единиц.
- Перемещение точки $C$ в точку $K$ составляет $12$ единиц, т.к. она сместилась вправо на $12$ единичных отрезков.