Как найти предел функции
Продемонстрируем, как графически найди предел любой функции, зная точку а, к которой стремится х.
Найти предел функции:
\[\mathop{\lim }\limits_{x\to 2} x^{2} \]Решение:
В приведенном выше примере х стремится к точке 2. Проведем через точку х=2 прямую линию, параллельную оси оY. Сразу же становится видно, что прямая пересекает график в точке y=4. Эта точка является тем предельным значением, к которому стремиться функция при стремлении x к числу 2. Другими словами, х не может принимать значения больше 2, значит, функция не пойдет дальше точки (2;4).
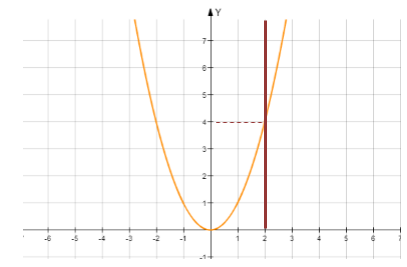
Рисунок 1. Предел функции $x^{2} $, при $x\to 2$
В общем случае решение пределов сводится в замене х числом или выражением а
\[\mathop{\lim }\limits_{x\to a} f(x)=\mathop{\lim }\limits_{x\to a} f(a)=b\]Вычислить предел функции
\[\mathop{\lim }\limits_{x\to 1} \frac{1}{2+x^{2} } =\frac{1}{2+1^{2} } =\frac{1}{3} \]Вычислить предел функции
\[\mathop{\lim }\limits_{x\to \infty } 3E^{3} =3*\infty ^{3} =\infty \]Вычислить предел функции
\[\mathop{\lim }\limits_{x\to \infty } (2E^{2} -3E)=2*\infty ^{2} -3*\infty =\left[\infty -\infty \right]\]В примере 4 получено выражение, которое невозможно упростить. Аналогичные решения называют неопределенностью.
Виды неопределенностей
\[\left[\frac{0}{0} \right];\left[\frac{\infty }{\infty } \right];\left[0^{0} \right];\left[1^{\infty } \right];\left[\infty ^{0} \right];\left[0\cdot \infty \right];\left[\infty -\infty \right]\]Это конечный ряд неопределенностей, которые могут возникнуть при решении, и его важно помнить!
От неопределенностей необходимо избавляться путем арифметических преобразований функции, к которым относятся:
- Упрощение (сокращение дробной функции)
- Разложение на множители
- Деление дробной функции
- Вынесение за скобку общего множителя и др.
Вернемся к примеру 4. Если вынести за скобку общий множитель х, получим:
\[\mathop{\lim }\limits_{x\to \infty } (2E^{2} -3E)=E(2E-3)=\infty (2*\infty -3)=\infty *\infty =\infty \]ЗАПОМНИМ:
\[\frac{1}{0} =\infty \]Рассмотрим операции по разрешению неопределенностей, наиболее часто встречающихся на практике.
Вычислить предел функции в точке
\[\mathop{\lim }\limits_{x\to 2} \frac{x^{2} -4}{x^{2} -2x} =\frac{2^{2} -4}{2^{2} -2*2} =\left[\frac{0}{0} \right]\]Получили неопределенность!
Решение:
- Разложим числитель (верхнюю строчку дроби) на множители. Для этого необходимо вспомнить формулу сокращенного умножения: \[(x-a)(x+a)=(x^{2} -a^{2} )\]
- В знаменателе вынесем за скобку неизвестное х \[\mathop{\lim }\limits_{x\to 2} \frac{\left(x-2\right)\left(x+2\right)}{x(x-2)} \]
- Сократим общий множитель (х-2) \[\mathop{\lim }\limits_{x\to 2} \frac{\left(x-2\right)\left(x+2\right)}{x(x-2)} =\mathop{\lim }\limits_{x\to 2} \frac{\left(x+2\right)}{x} =\frac{\left(2+2\right)}{2} =2\]
По которой
\[(x-2)(x+2)=(x^{2} -4)\]Предел разрешился и равен 2
Вычислить предел
\[\mathop{\lim }\limits_{x\to \frac{\pi }{2} } \frac{\sin x-\cos x}{ctgx-1} =\mathop{\lim }\limits_{x\to \frac{\pi }{2} } \frac{\sin x-\cos x}{\frac{\cos x}{\sin x} -\frac{\sin x}{\sin x} } =\mathop{\lim }\limits_{x\to \frac{\pi }{2} } \frac{\sin x-\cos x}{\frac{\cos x-\sin x}{\sin x} } =\mathop{\lim }\limits_{x\to \frac{\pi }{2} } \frac{(\sin x-\cos x)*\sin x}{-(\sin x-\cos x)} =\frac{\sin x}{-1} =-1\]Число b является пределом функции f(x) в точке a, если для любой сходящейся к а последовательности $\{xn\}$ такой, что $x_{n} \in X ,x_{n} \ne 0$ последовательность $\{f (xn)\}$ сходится к b.
Данное определение и связанные с ним доказательства практически не используются. Важно запомнить, что понятие предел функции в точке а вводится только для предельных точек а области определения функции. При этом а может и не принадлежать Х.
Число b называется пределом функции f(x) в точке а (если х стремится к этой точке), если $\forall \varepsilon >0_{}^{} \exists \delta >0$ такое, что $\forall x$,удовлетворяющего условиям $x\backepsilon X$,
$0
Доказать по определению Коши, что
\[\mathop{\lim }\limits_{x\to 4} \frac{x^{2} -16}{x^{2} -4x} =2\]Решение:
- Определяем функцию \[f(x)=\frac{x^{2} -16}{x^{2} -4x} \]
- Из условия предел стремится к 4, значит, необходимо рассмотреть окрестность данной точки. Например, все точки на промежутке (2;5). Не забываем, что функция не определена в точках 0 и 4 (ОДЗ по знаменателю).
- Запишем условие по Коши \[\forall \varepsilon >0_{}^{} \exists \delta >0:\forall E\ne 4,\left|E-4\right|Полученное выражение означает необходимость найти такое $\delta $, при котором х будет отлично от 4 и $\left|E-4\right|$, которое не больше $\delta \Rightarrow \left|f(x)-2\right|$
- Преобразуем выражение \[\left|f(x)-2\right|,x\ne 4\] \[\left|f(x)-2\right|=\left|\frac{x^{2} -16}{x^{2} -4x} -2\right|=\left|\frac{(x-4)(x+4)}{x(x-4)} -2\right|=\left|\frac{(x+4)}{x} -2\right|=\frac{\left|x-4\right|}{x} \]
- Зададим $\delta =2\varepsilon $(т.к. точка равна 2). Получим: \[\begin{array}{l} {\forall x\backepsilon (2;5)} \\ {0












