
Что такое бесконечно малая величина
Понятие бесконечно малой величины тесно связано с понятием предела.
Бесконечно малой величиной называют числовые функции или последовательности, бесконечно стремящиеся к нулю.
Проследим изменение бесконечно малых на рисунках 1 и 2.
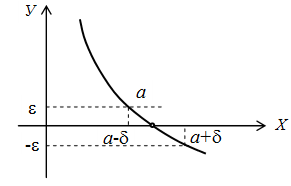
Рисунок 1. Функция y = f (x) пересекает ось Ох
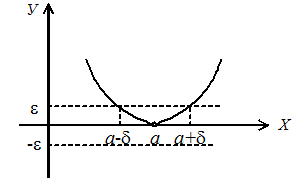
Рисунок 2. Функция y = f (x) касается оси Ох в точке х = а
Что такое исчисление бесконечно малых величин
Вычисления с бесконечно малыми величинами, при которых результатом является бесконечно непрерывная сумма бесконечно малых, называют исчислением бесконечно малых величин.
Бесконечно малой последовательностью является такая последовательность an, для которой выполняется равенство:
limРассмотрим последовательность
\frac{1}{n} =\frac{1}{2} ,\frac{1}{3} ,\frac{1}{4} ...\frac{1}{n}Последовательность бесконечно убывает, а значит, является бесконечно малой величиной.
Функция называется бесконечно малой в окрестности точки х0, если выполняется условие:
\mathop{\lim }\limits_{n\to x_{0} } f(x)=0Функция называется бесконечно малой на бесконечности, если выполняется одно из условий:
\mathop{\lim }\limits_{n\to \infty } f(x)=0; \mathop{\lim }\limits_{n\to -\infty } f(x)=0Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если:
\mathop{\lim }\limits_{n\to \infty } f(x)=a, то f(x)-a=a(x) , \mathop{\lim }\limits_{n\to \infty } \left(f(x)-a\right)=0Бесконечно малая величина является переменной величиной, которая будет меньше числа \varepsilon лишь в результате своего стремления х к а.
\mathop{\lim }\limits_{n\to a} f(x)=0Функция y = f (x) называется бесконечно малой (при x>+∞), если каково бы ни было {\mathbf \varepsilon } > 0, можно найти такое число N, что при всех x > N выполняется неравенство:
\[\left|f(x)\right|Доказать, что функция
y=\frac{1}{x^{2} }является бесконечно малой при x>+∞.
Доказательство: Определим, что при x>+∞ предел функции b=0, т.е. что для любого \varepsilon > 0 можно найти такое N, что при x > N выполняется неравенство:
\left|f(x)\right|=\left|\frac{1}{x^{2} } \right|=\frac{1}{x^{2} } Данное неравенство справедливо только если \[x>\frac{1}{\sqrt{\varepsilon } } =NАналогично для функции вида
y=\frac{1}{x^{a} } (а -- любое положительное число)
Справедливо утверждение, что функция бесконечно малая.
Докажем, что функция y = x^3 является бесконечно малой при x > 0.
Доказательство: Зададим \varepsilon > 0. Неравенство |f(x)| = |x3| \[\left|x\right|Таким образом, неравенство |x^3| N=-\sqrt[{3}]{\varepsilon } \begin{array}{cc} {} & {\begin{array}{cc} {8} & {M=\sqrt[{3}]{\varepsilon } } \end{array}} \end{array}
Это значит, что
\mathop{\lim }\limits_{x\to 0} x^{3} =0т.е. функция y = x^3 бесконечно малая при x > 0.
Определим, является ли бесконечно малой при x > +∞ функция:
y=2-\frac{1}{x}Решение:
\mathop{\lim }\limits_{x\to +\infty } \left(2-\frac{1}{x} \right)=2-0=2\ne 0Ответ: Функция не является бесконечно малой при x > +∞.
Свойства бесконечно малых
- Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
- Произведение бесконечно малых --- бесконечно малая.
- Произведение бесконечно малой последовательности на ограниченную (или константу) --- бесконечно малая.
- Если a_n --- бесконечно малая последовательность, сохраняющая знак, то b_n=1 / a_n --- бесконечно большая последовательность.
Докажем, что функция
y=\frac{1}{x} +\frac{1}{\sqrt{x} } +\frac{1}{x^{2} }Является бесконечно малой функцией при x > +∞.
Доказательство: Так как каждое слагаемое функции является бесконечно малой при x > +∞ (см. пример 2), по свойству 1 -- функция является бесконечно малой величиной.



















