Определение нормального распределения.
Случайная величина $X$ имеет нормальное распределение, если плотность её распределения определяется формулой:
\[\varphi \left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-{(x-a)}^2}{2{\sigma }^2}}\]где $a?R$, а $\sigma >0$ -- константы.
Разберем теперь, какой смысл имеют константы $a$ и $\sigma $.
Для этого попробуем найти числовые характеристики для данного распределения. Начнем с математического ожидания.
Сделаем замену: $\frac{x-a}{\sigma }=t,\ x=\sigma t+a,\ dx=\sigma dt$.
$\frac{1}{\sqrt{2\pi }}\int\limits^{+\infty }_{-\infty }{e^{\frac{-t^2}{2}}dt}$ - это функция плотности распределения некоторой случайной величины, следовательно:
Из этого сего получим:
!!! То есть константа $a$ в определении 1 -- это математическое ожидание данного распределения.
Найдем теперь дисперсию:
Сделаем замену: $\frac{x-a}{\sigma }=t,\ x=\sigma t+a,\ dx=\sigma dt$.
Используя вычисления неопределенного интеграла и тот факт, что $\frac{1}{\sqrt{2\pi }}\int\limits^{+\infty }_{-\infty }{e^{\frac{-t^2}{2}}dt}=1$, то есть $\int\limits^{+\infty }_{-\infty }{e^{\frac{-t^2}{2}}dt}=\sqrt{2\pi }$, получим:
Найдем теперь среднее квадратическое отклонение:
!!! То есть константа $\sigma $ в определении 1 -- это среднее квадратическое отклонение данного распределения.
Нормальная кривая
Нормальной кривой (или кривой Гаусса) называется график функции плотности нормального распределения $\varphi (x)$
Исследуем данную функцию и определим вид ее графика:
-
Область определения: $\left(-\infty ,+\infty \right)$.
-
Область значения: $(0,\ \frac{1}{\sqrt{2\pi }\sigma }]$.
-
$\varphi \left(x\right)>0,$ график функции расположен выше оси $Ox)$
-
При $x=0,$ $\varphi \left(0\right)=\frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-{(0-a)}^2}{2{\sigma }^2}}=\frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-a^2}{2{\sigma }^2}}$.\
-
$\varphi \left(x\right)$ непрерывна на всей области определения.
-
$\varphi '\left(x\right)={\left(\frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-{\left(x-a\right)}^2}{2{\sigma }^2}}\right)}'=-\frac{x-a}{\sqrt{2\pi }{\sigma }^3}\cdot e^{\frac{-{\left(x-a\right)}^2}{2{\sigma }^2}}$
Точка $(a,\ \frac{1}{\sqrt{2\pi }\sigma })$ -- точка максимума.
Функция $\varphi \left(x\right)$ убывает, при $x>a$, и возрастает, при $x
-
График симметричен относительно прямой $x=a$.
-
$\varphi ''\left(x\right)={\left(-\frac{x-a}{\sqrt{2\pi }{\sigma }^3}\cdot e^{\frac{-{\left(x-a\right)}^2}{2{\sigma }^2}}\right)}'=-\frac{1}{\sqrt{2\pi }{\sigma }^3}\cdot e^{\frac{-{\left(x-a\right)}^2}{2{\sigma }^2}}\cdot \left(1-\frac{{\left(x-a\right)}^2}{{\sigma }^2}\right)$
Функция $\varphi \left(x\right)$ имеет точки перегиба при $x=a\pm \sigma $.
- Примерный вид кривой (рис. 1):
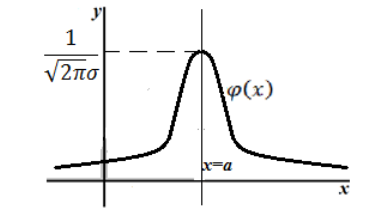
Рисунок 1. График плотности нормального распределения.
Пример задач на нормальное распределение вероятности
Нормальное распределение вероятности задана следующей функцией плотности распределения:
\[\varphi \left(x\right)=\frac{1}{0,3\sqrt{2\pi }}e^{\frac{-{(x-2)}^2}{2{\sigma }^2}}\]Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение.
Решение:
Используя определение 1 сразу найдем
Математическое ожидание: $M\left(X\right)=a=2$.
Среднее квадратическое распределение: $\sigma \left(X\right)=\sigma =0,3$.
Тогда получим, что дисперсия: $D\left(X\right)={\sigma }^2$=0,09.
Длина стержня $X$ представляет собой случайную непрерывную величину. $X$ распределена по нормальному закону распределения среднее значение которого равно $30$ мм, а среднее квадратическое отклонение равно $0,2$ мм. Найти плотность распределения такой случайной величины и построить её график:
Решение:
Из условия имеем: $a=30,\ \sigma =0,2$.
Тогда по определению 1, получим:
\[\varphi \left(x\right)=\frac{1}{0,2\sqrt{2\pi }}e^{\frac{-{(x-30)}^2}{0,08}}\]Найдем точку максимума: $\left(a,\ \frac{1}{\sqrt{2\pi }\sigma }\right)=\left(30,\frac{1}{0,2\sqrt{2\pi }}\right)$
График имеет вид:
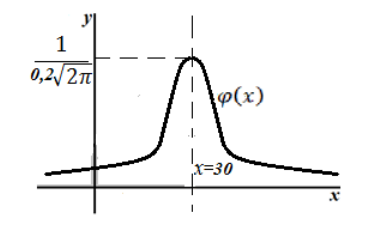
Рисунок 2.












