Для квадратной матрицы в теории матриц вводятся понятия «минор элемента» и «алгебраическое дополнение».
Минор $M_{ij} $ элемента $a_{ij} $ матрицы $A=\left(a_{ij} \right)_{n\times n} $ - это определитель матрицы, которая образована после вычеркивания из исходной матрицы строки с номером $i$ и столбца с номером $j$.
Выписать и вычислить миноры элементов $a_{11} $ и $a_{22} $ матрицы $A=\left(\begin{array}{ccc} {1} & {9} & {-2} \\ {0} & {-3} & {2} \\ {1} & {3} & {4} \end{array}\right)$.
Решение:
\[M_{11} =\left|\begin{array}{cc} {-3} & {2} \\ {3} & {4} \end{array}\right|=-3\cdot 4-3\cdot 2=-12-6=-18;\] \[M_{22} =\left|\begin{array}{cc} {1} & {-2} \\ {1} & {4} \end{array}\right|=1\cdot 4-1\cdot (-2)=4+2=6.\]Алгебраическое дополнение $A_{ij} $ элемента $a_{ij} $ матрицы $A=\left(a_{ij} \right)_{n\times n} $ определяется следующей формулой:
\[A_{ij} =(-1)^{i+j} \cdot M_{ij} ,\]где $M_{ij} $ - минор соответствующего элемента матрицы.
Найти алгебраические дополнения элементов $a_{11} $ и $a_{22} $ матрицы $A=\left(\begin{array}{ccc} {1} & {9} & {-2} \\ {0} & {-3} & {2} \\ {1} & {3} & {4} \end{array}\right)$.
Решение:
\[A_{11} =(-1)^{1+1} \cdot M_{11} =1\cdot \left|\begin{array}{cc} {-3} & {2} \\ {3} & {4} \end{array}\right|=-3\cdot 4-3\cdot 2=-12-6=-18;\] \[A_{22} =(-1)^{2+2} \cdot M_{22} =1\cdot \left|\begin{array}{cc} {1} & {-2} \\ {1} & {4} \end{array}\right|=1\cdot 4-1\cdot (-2)=4+2=6.\]Для прямоугольной матрицы вводится понятие «минор k-го порядка».
Минор k-го порядка матрицы $A=\left(a_{ij} \right)_{m\times n} $ - это определитель матрицы, которая образована из исходной матрицы путем выписывания элементов, находящихся на пересечении k строк и k столбцов.
Схема формирования минора 3-го порядка изображена на рисунке.
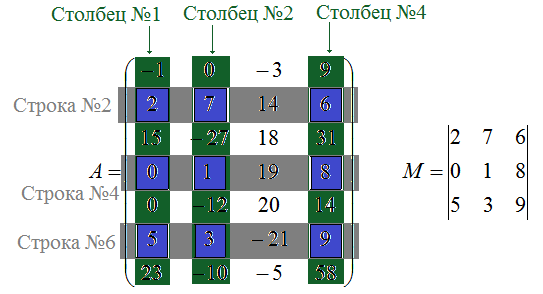
Найти миноры 1-го и 2-го порядков матрицы $A=\left(\begin{array}{ccc} {1} & {9} & {-2} \\ {0} & {-3} & {2} \\ {1} & {3} & {4} \end{array}\right)$.
Решение:
$M=\left|1\right|=1$ (пересечение первой строки с первым столбцом);
$M=\left|\begin{array}{cc} {1} & {9} \\ {1} & {3} \end{array}\right|=1\cdot 3-1\cdot 9=3-9=-6$ (пересечение первой и третьей строк с первым и вторым столбцами).
Из примера видно, что миноры первого порядка совпадают с элементами исходной матрицы.
Главный минор -- это минор k-го порядка матрицы $A=\left(a_{ij} \right)_{m\times n} $, в котором на главной диагонали расположены только элементы главной диагонали исходной матрицы.
Найти главные миноры 2-го порядков матрицы $A=\left(\begin{array}{ccc} {1} & {9} & {-2} \\ {0} & {-3} & {2} \\ {1} & {3} & {4} \end{array}\right)$.
Решение:
$M=\left|\begin{array}{cc} {1} & {9} \\ {0} & {-3} \end{array}\right|=1\cdot (-3)-0\cdot 9=-3$ (пересечение первой и второй строки, первого и второго столбца).
$M=\left|\begin{array}{cc} {1} & {-2} \\ {1} & {4} \end{array}\right|=1\cdot 4-1\cdot (-2)=4+2=6$ (пересечение первой и третьей строки, первого и третьего столбца).
Базисный минор k-го порядка матрицы $A=\left(a_{ij} \right)_{m\times n} $ - это такой не равный нулю минор, что все миноры порядка выше k обращаются в ноль.
Найти базисный минор 2-го порядка матрицы $A=\left(\begin{array}{ccc} {1} & {0} & {-2} \\ {0} & {0} & {2} \\ {0} & {0} & {0} \end{array}\right)$.
Решение:
$M=\left|\begin{array}{cc} {1} & {-2} \\ {0} & {2} \end{array}\right|=1\cdot 2-0\cdot (-2)=2-0=2$ (пересечение первой и второй строки, первого и третьего столбца).
Любой минор 3-го порядка совпадает с исходной матрицей. Так как матрица имеет нулевой столбец, то ее определитель равен нулю. Следовательно, найденный минор является базисным.
Дополнительный минор (n-k)-го порядка матрицы $A=\left(a_{ij} \right)_{m\times n} $ - это такой минор, элементы которого выписаны из исходной матрицы после вычеркивания строк и столбцов, содержащих минор М.
Найти дополнительный минор для минора 2-го порядка матрицы $A=\left(\begin{array}{cccc} {1} & {2} & {0} & {-3} \\ {4} & {2} & {1} & {-5} \\ {0} & {2} & {-1} & {3} \\ {0} & {1} & {0} & {3} \end{array}\right)$.
Решение:
$M=\left|\begin{array}{cc} {1} & {2} \\ {4} & {2} \end{array}\right|=1\cdot 2-4\cdot 2=2-8=-6$ (пересечение первой и второй строки, первого и второго столбца).
$M'=\left|\begin{array}{cc} {-1} & {3} \\ {0} & {3} \end{array}\right|=-1\cdot 3-0\cdot 3=-3$ - дополнительный минор











