Иррациональные уравнения
Рассмотрим теперь понятие рационального неравенства.
Уравнение, в котором неизвестная величина находится под радикалами или в дробных степенях будем называть иррациональным.
Здесь надо всегда помнить о том, что не под любым корнем может быть отрицательное число. В связи с этим здесь будет появляться понятие области определения уравнения (ООУ). Оно заключается в том, что под корнями с четными степенями не может быть отрицательных величин.
Решение классических иррациональных уравнений заключается в следующем: Вначале мы находим ООУ, с помощью простейших преобразований приводим уравнение к виду $\sqrt[n]{P(x)}=\sqrt[n]{Q(x)}$. Возводим в $n$-ю степень и находим корни получившегося уравнения. Выкидываем корни, не попадающие в ООУ.
Пример решения иррационального уравнения
Решить
$\sqrt[5]{x^2-4x+4}-\sqrt[5]{x-2}=2$
Решение.
Применяя формулу квадрата суммы, получим:
$\sqrt[5]{(x-2)^2}-\sqrt[5]{x-2}-2=0$
Так как степень корня нечетна, то нам здесь не требуется нахождения ООУ.
Сделаем замену $\sqrt[5]{x-2}=t$, получим
$t^2-t+2=0$
Это уравнение имеет своими корнями числа $-1$ и $-2$.
Получим два уравнения:
$\sqrt[5]{x-2}=-1$ и $\sqrt[5]{x-2}=-2$
$x-2=-1$ и $x-2=-32$
$x=1$ и $x=-30$
Ответ: $1$ и $-30$.
Иррациональные неравенства
Рассмотрим теперь понятие иррационального неравенства.
Неравенство, которое имеет вид $\sqrt[n]{P(x)}>(≥)\sqrt[n]{Q(x)}$ будем называть иррациональным неравенством.
Чаще всего неравенства решаются методом промежутков (интервалов). В основе этого метода лежит следующее рассуждение.
Пусть нам дана функция $f(x)=\frac{(x-n)(x-m)}{(x-l)(x-k)}$, причем $n
$x∈(-∞,n)$: Используя неравенство (1) будем получать:
$(x-n)
Четыре минуса, в общем, нам дадут плюсовое значение, то есть $f(x)>0$.
$x∈(n,m)$:
Используя неравенство (1) будем получать:
$(x-n)>0,(x-m)
Три минуса, в общем, нам дадут минусовое значение, то есть $f(x)
$x∈(m,l)$:
Используя неравенство (1) будем получать:
$(x-n)>0,(x-m)>0,(x-l)0$.
$x∈(l,k)$:
Используя неравенство (1) будем получать:
$(x-n)>0,(x-m)>0,(x-l)>0,(x-k)
Один минус дает нам минусовое значение, то есть $f(x)
$x∈(k,+∞)$:
Используя неравенство (1) будем получать:
$(x-n)>0,(x-m)>0,(x-l)>0,(x-k)>0$.
Все плюсы нам дадут плюсовое значение, то есть $f(x)>0$
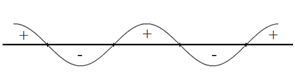
Это рассуждение можно иллюстрировать на числовой прямой (рис. 1).
Эта иллюстрация называется кривой знаков и используется для решения рациональных и других неравенств $q(x)>(≥)0$ методом промежутков.
На самом деле знаки на такой кривой не всегда чередуются. К примеру такое может быть при наличии в уравнение квадратного множителя.
Суммируя, получим:
Метод промежутков (интервалов)
- Вначале необходимо найти все корни уравнения $q(x)=0$ и значения, в которых область определения имеет разрыв.
- И всех полученных в пункте $1$ числовых значений составляем кривую знаков для данного уравнения.
- Записываем ответ из кривой знаков, с учетом знака неравенства.
Пример решения иррационального неравенства методом промежутков
Решить
$\sqrt[4]{z-1}≤\sqrt[8]{z+5}$
Решение.
Найдем ООУ:
$z-1 ≥0$ и $z+5 ≥0$
$z ≥1$ и $z ≥-5$
ООУ: $[1,∞)$.
Решим для начала следующее уравнение и найдем точки разрыва ее области определения:
$\sqrt[4]{z-1}-\sqrt[8]{z+5}=0$
$\sqrt[4]{z-1}=\sqrt[8]{z+5}$
$z^2-2z+1=z+5$
$z^2-3z-4=0$
Корни: $z=-1$ и $z=4$
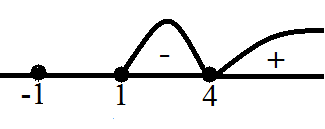
Изобразим все полученные точки и ООУ на числовой прямой и построим кривую знаков:
Так как у нас знак неравенства «меньше или равно», то нам нужно выбрать промежуток со знаком минус.
Ответ: $[1,4]$.