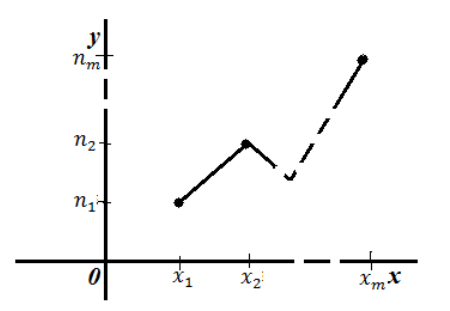
Полигон частот
Пусть нам дан ряд распределения, записанный с помощью таблицы:
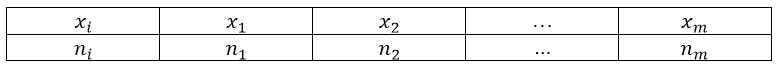
Рисунок 1.
Помимо обычной частоты существует еще понятие относительной частоты.
Получаем следующую таблицу распределения относительных частот:
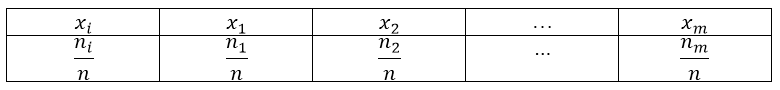
Рисунок 3.
Полигон относительных частот -- ломанная, которая соединяет точки $(x_m,W_m)$ ($m=1,2,\dots ,m)$.
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие относительные частоты. Полученные точки соединяют ломанной:
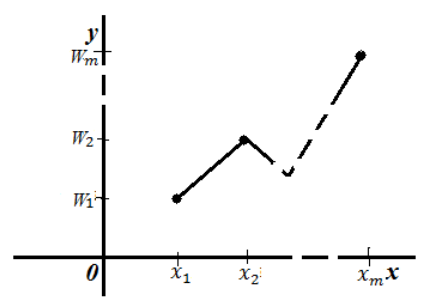
Рисунок 4. Полигон относительных частот.
Гистограмма частот
Помимо понятия полинома для непрерывных значений существует понятие гистограммы.
Гистограмма частот -- ступенчатая фигура, состоящая из прямоугольников с основанием -- частичными интервалами длины $h$ и высотами $\frac{n_i}{h}$:
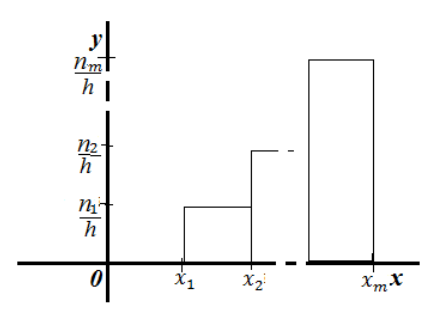
Рисунок 5. Гистограмма частот.
Заметим, что площадь одного такого прямоугольника $\frac{n_ih}{h}=n_i$. Следовательно, площадь всей фигуры равна $\sum{n_i}=n$, то есть равна объему выборки.
Гистограмма относительных частот -- ступенчатая фигура, состоящая из прямоугольников с основанием -- частичными интервалами длины $h$ и высотами $\frac{W_i}{h}$:
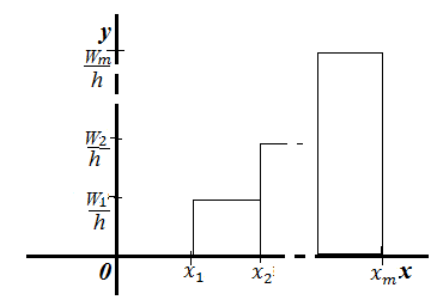
Рисунок 6. Гистограмма относительных частот.
Заметим, что площадь одного такого прямоугольника $\frac{W_ih}{h}=W_i$. Следовательно, площадь всей фигуры равна $\sum{W_i}=W=1$.
Примеры задачи на построение полигона и гистограммы
Пусть распределение частот имеет вид:

Рисунок 7.
Построить полигон относительных частот.
Решение.
Построим сначала ряд распределения относительных частот по формуле $W_i=\frac{n_i}{n}$

Рисунок 8.
Получим следующий полигон относительных частот.
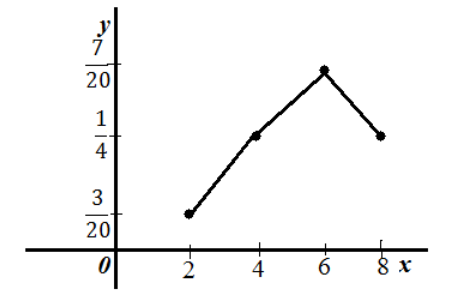
Рисунок 9.
Дан ряд непрерывного распределения частот:

Рисунок 10.
Решение.
Очевидно, что данном случае длина частичного интервала $h=2.$ Найдем высоты прямоугольников каждой точки разбиения.
При $x=1$: $\frac{3}{2}=1,5$.
При $x=3$: $\frac{5}{2}=2,5.$
При $x=6$: $\frac{7}{2}=3,5.$
При $x=9$: $\frac{9}{2}=4,5.$
Получаем следующую гистограмму частот:
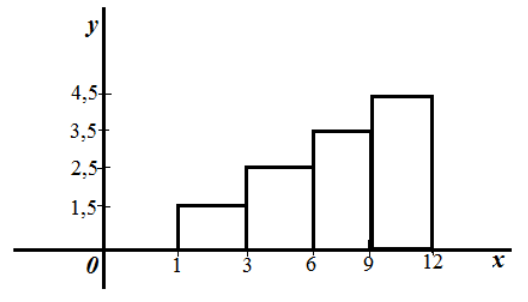
Рисунок 11.