Дисперсией $D\xi \, $ случайной величины $\xi$ называется математическое ожидание квадрата ее отклонения, то есть $D\xi =M(\xi -M\xi )^{2} \, $ (если соответствующее математическое ожидание существует).
Пользуясь свойствами математического ожидания случайной величины и преобразуем формулу:
то есть, получаем
Тогда дисперсия случайной величины вычисляется по формуле:
$D\xi =\sum \limits _{i=1}^{n}x_{i}^{2} \cdot p_{i} -M^{2} \xi $, если $\xi$ - дискретная случайная величина;
$D\xi =\int \limits _{-\infty }^{\infty }x^{2} \cdot \rho (x) dx-M^{2} \xi $, если $\xi$ - непрерывная случайная величина.
Свойства дисперсии
-
$D\xi \ge 0\, $ для любой случайной величины $\xi$.
-
$Dc=0\, $, если $c=const\, $.
-
$D(c\cdot \xi )=c^{2} \cdot D\xi \, $, если $c=const\, $.
-
$D(\xi \pm \eta )=D\xi +D\eta \, $, если $\xi$, $\eta$ - независимые случайные величины.
Применение на практике
В ящике среди $20$ деталей находится $8$ стандартных. Извлекается $3$ детали. Случайная величина $\xi$ - число нестандартных деталей в выборке. Требуется:
-
построить ряд распределения величины $\xi$;
-
найти функцию распределения $F_{\xi } (x)$, построить ее график;
-
найти $M\xi $, $D\xi $.
Решение. Так как случайная величина $\xi$ -- число нестандартных деталей в выбранных $3-х$ деталях, то она может принимать только значения $0, 1, 2, 3$. Составим ряд распределения (рис. 1) этой случайной величины
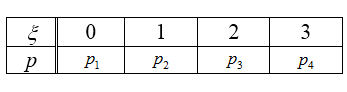
Рисунок 1.
Вычислим вероятности, входящие в ряд распределения:
\[p_{1} =P(\xi =0)=\frac{C_{8}^{3} \cdot C_{12}^{0} }{C_{20}^{3} } =\frac{8\cdot 7\cdot 6\cdot 3!}{3!\cdot 20\cdot 19\cdot 18} =\frac{14}{285} ;\] \[p_{2} =P(\xi =1)=\frac{C_{8}^{2} \cdot C_{12}^{1} }{C_{20}^{3} } =\frac{8\cdot 7\cdot 12\cdot 3!}{2!\cdot 20\cdot 19\cdot 18} =\frac{84}{285} ;\] \[p_{3} =P(\xi =2)=\frac{C_{8}^{1} \cdot C_{12}^{2} }{C_{20}^{3} } =\frac{8\cdot 12\cdot 11\cdot 3!}{2!\cdot 20\cdot 19\cdot 18} =\frac{132}{285} ;\] \[p_{4} =P(\xi =3)=\frac{C_{8}^{0} \cdot C_{12}^{3} }{C_{20}^{3} } =\frac{12\cdot 11\cdot 10\cdot 3!}{3!\cdot 20\cdot 19\cdot 18} =\frac{55}{285} .\]Ряд распределения (рис. 2) случайной величины $\xi$ имеет вид
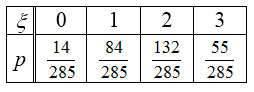
Рисунок 2.
Найдем функцию распределения $F_{\xi } (x)\, $. По определению имеем
\[F_{\xi } (x)=P(\xi Значения случайной величины $\xi$ разбивают действительную ось на 5 интервалов. Будем фиксировать x в каждом из этих интервалов.Пусть $x\le 0$, тогда $F_{\xi } (x)=P(\xi
$0 \[F_{\xi } (x)=P(\xi $1 \[F_{\xi } (x)=P(\xi $2
$F_{\xi } (x)=P(\xi \[=P(\xi =0)+P(\xi =1)+P(\xi =2)=\frac{14}{285} +\frac{84}{285} +\] \[\frac{132}{285} =\frac{230}{285} \, ;\]
$x>3\, $, тогда $F_{\xi } (x)=P(\xi \[\xi =3)=P(\xi =0)+P(\xi =1)+P(\xi =2)+\] \[+P(\xi =3)=\frac{14}{285} +\frac{84}{285} +\frac{132}{285} +\frac{55}{285} =1\, .\]
Окончательно получаем (рис. 3)
\[F_{\xi } (x)=\left\{\begin{array}{l} {0,{\rm \; \; \; \; \; \; \; \; \; \; \; \; \; }x\le 0;} \\ {14/285,{\rm \; \; \; \; }03.} \end{array}\right. \, \]
Рисунок 3.
Найдем (по определению) математическое ожидание и дисперсию
\[M\xi =\sum \limits _{i=1}^{4}x_{i} \cdot p_{i} =0\cdot \frac{14}{285} +1\cdot \frac{84}{285} +2\cdot \frac{132}{285} +3\cdot \frac{55}{285} =\frac{513}{285} =\, \] \[=\frac{3\cdot 19\cdot 9}{3\cdot 19\cdot 5} =\frac{9}{5} =1,8\, ;\] \[D\xi =\sum \limits _{i=1}^{4}x_{i} ^{2} \cdot p_{i} -M^{2} \xi =0\cdot \frac{14}{285} +1\cdot \frac{84}{285} +4\cdot \frac{132}{285} +9\cdot \frac{55}{285} -\, \] \[-\left(\frac{9}{5} \right)^{2} =\frac{1107}{285} -\frac{81}{25} =\frac{3\cdot 41\cdot 9}{3\cdot 19\cdot 5} -\frac{81}{25} =\frac{41\cdot 9}{19\cdot 5} -\frac{81}{5\cdot 5} =\, \] \[=\frac{41\cdot 9\cdot 5-81\cdot 19}{19\cdot 5\cdot 5} =\frac{306}{475} \approx 0,631\, .\]










