Упрощение логических выражений — это формирование замены логических выражений на равнозначные на основе законов алгебры логики, для того чтобы получить высказывания, имеющие более простую форму.
Общие сведения о логике
Термином «логика» принято обозначать науку, которая занимается изучением правил и законов мышления, методик нахождения доказательств и опровержением различных предположений. Основоположником логики является древнегреческий философ Аристотель, живший в четвертом веке до нашей эры. Сначала он отметил, что при попытке доказать какие-либо положения на базе других положений, за основу принимают не заложенное в них фактическое содержание, а лишь их взаимные отношения форм. Другой древнегреческий ученый, Евклид, сумел систематизировать большое количество положений геометрии с позиций логики. Евклид сформулировал так называемый метод аксиом и положил начало восприятию геометрии как науки, базирующейся на аксиомах.
Набор логически постулаты Аристотеля подвергался различным модификациям в течение длительного времени. Существенным качественным скачком в развитии логической науки явилось привлечение в логику математических методов. Положил начало этой тенденции знаменитый немецкий ученый Г. Лейбниц, который жил в семнадцатом и восемнадцатом веках нашей эры. Он пытался выработать универсальный языковый формат, который позволил бы формализовать разнообразные выкладки и все разногласия, и споры привести к виду математических формул.
Возникновение науки, именуемой математической логикой, сопряжено с работами английского ученого Джона Буля. Он является автором алгебры логики, впоследствии получившей наименование Булева алгебра. Она стала результатом применения в логике алгебраических методик.
Упрощение логических выражений
Логическим выражением является символьная запись, которая состоит из логических величин (констант или переменных), объединяемых логическими операциями (связками). В булевой алгебре простому высказыванию ставится в соответствие логическая переменная, значение которой равняется единице, когда высказывание является истинным, и нулю, когда высказывание является ложным. Обозначать логические переменные принято буквами латинского алфавита.
Известны различные варианты обозначений истинности и ложности переменных. В русскоязычном варианте символы "НЕ", "И", "ИЛИ" обозначают логические операции инверсию, конъюнкцию и дизъюнкцию. Эти операции являются основными логическими операциями, с помощью которых может быть записано любое логическое выражение.
Конъюнкцией двух высказываний является новое высказывание, принимающее значение истинно, когда оба высказывания являются истинными, в противном случае высказывание является ложным.
Конъюнкция, или логическое умножение, или логическое «И», может быть обозначена следующими образами:
- ∧ , к примеру, А ∧ В.
- &, к примеру, А & В.
- В языках программирования как «And».
Дизъюнкцией двух высказываний является новое высказывание, принимающее значение истина, когда хотя бы одно из высказываний является истинным, в противном случае высказывание является ложным.
Операция дизъюнкции, или логического сложения, или логического «ИЛИ» может обозначаться следующим образом:
- ∨, к примеру, А ∨ В.
- В языках программирования как «Or».
Инверсией двух высказываний является новое высказывание, которое является истинным только в том случае, когда исходное высказывание является ложным.
Операция инверсии может обозначаться следующим образом:
- В естественном языке это может быть выражение «неверно, что...» и частица «не».
- В алгебре высказываний обозначается как «¬» или «-».
- В языках программирования используется обозначение «Not».
В алгебре логики логическим связкам соответствуют логические операции, которые обладают специальными названиями и могут обозначаться следующим образом.

Рисунок 1. Таблица. Автор24 — интернет-биржа студенческих работ
Рассмотрим примеры использования правил алгебры логики, позволяющих упростить логические выражения. Предположим, что необходимо определить кто из подозреваемых принимал участие в преступлении, если достоверно известными являются следующие факты:
- Если Иванов или Петров не принимали участия в преступлении, то тогда Сидоров точно принимал участие.
- Если Иванов не принимал участие в преступлении, то тогда и Сидоров не принимал участия в преступлении.
Для того чтобы решить эту логическую задачу, введем следующие обозначения:
- И, означает, что Иванов принимал участие в преступлении.
- П, означает, что Петров принимал участие в преступлении.
- С, означает, что Сидоров принимал участие в преступлении.
Сформируем выражения для каждого из исходных утверждений (высказываний):
- $(( \bar И + П) →С)$
- $(\bar И → \bar С )$
Объединим два этих утверждения в единое высказывание:
$(( \barИ + П) →С)$ & $(\bar И → \bar С )$
Сформируем таблицу истинности на данное логическое выражение.

Рисунок 2. Таблица. Автор24 — интернет-биржа студенческих работ
В результате получаем, что лишь у Иванова в сформированных строках "ИСТИНА" совпадает с его участием в преступлении. То есть, получается, что Иванов и является преступником. А другие подозреваемые или не были участниками преступления, или на них недостаточно улик, чтобы их обвинить.
Рассмотрим еще один пример. У троих друзей, которые являются болельщиками автогонок «Формула-1», возник спор об итогах очередного этапа гонок. Они сделали следующие предположения:
- Ш - победителем будет Шумахер.
- Х - победит Хилл.
- А - победителем будет Ализи.
Высказывания каждого из друзей зафиксированы ниже.

Рисунок 3. Высказывания. Автор24 — интернет-биржа студенческих работ
Если учесть, что предположения двух друзей подтвердились, а предположения третьего оказались неверными, можно представить и упростить истинное высказывание:
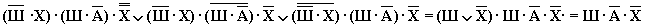
Рисунок 4. Ввысказывание. Автор24 — интернет-биржа студенческих работ
Победил Шумахер.











