Если вы хотите перевести число из одной системы счисления в другую, то удобнее для начала перевести его в десятичную систему счисления, и уже только потом из десятичной перевести в любую другую систему счисления.
Правила перевода чисел из любой системы счисления в десятичную
В вычислительной технике, использующей машинную арифметику, большую роль играет преобразование чисел из одной системы счисления в другую. Ниже приведем основные правила таких преобразований (переводов).
-
При переводе двоичного числа в десятичное требуется представить двоичное число в виде многочлена, каждый элемент которого представлен в виде произведения цифры числа и соответствующей степени числа основания, в данном случае $2$, а затем нужно вычислить многочлен по правилам десятичной арифметики:
$X_2=A_n \cdot 2^{n-1} + A_{n-1} \cdot 2^{n-2} + A_{n-2} \cdot 2^{n-3} + ... + A_2 \cdot 2^1 + A_1 \cdot 2^0$
При переводе рекомендуется для удобства использовать таблицу 1.

Рисунок 1. Таблица 1
Число $11110101_2$ перевести в десятичную систему счисления.
Решение. Используя приведенную таблицу $1$ степеней основания $2$, представим число в виде многочлена:
$11110101_2 = 1 \cdot 27 + 1 \cdot 26 + 1 \cdot 25 + 1 \cdot 24 + 0 \cdot 23 + 1 \cdot 22 + 0 \cdot 21 + 1 \cdot 20 = 128 + 64 + 32 + 16 + 0 + 4 + 0 + 1 = 245_{10}$
-
Для перевода числа из восьмеричной системы счисления в десятичную требуется представить его в виде многочлена, каждый элемент которого представлен в виде произведения цифры числа и соответствующей степени числа основания, в данном случае $8$, а затем нужно вычислить многочлен по правилам десятичной арифметики:
$X_8 = A_n \cdot 8^{n-1} + A_{n-1} \cdot 8^{n-2} + A_{n-2} \cdot 8^{n-3} + ... + A_2 \cdot 8^1 + A_1 \cdot 8^0$
При переводе рекомендуется использовать таблицу 2.

Рисунок 2. Таблица 2
Число $75013_8$ перевести в десятичную систему счисления.
Решение. Используя приведенную таблицу $2$ степеней основания $8$, представим число в виде многочлена:
$75013_8 = 7\cdot 8^4 + 5 \cdot 8^3 + 0 \cdot 8^2 + 1 \cdot 8^1 + 3 \cdot 8^0 = 31243_{10}$
-
Для перевода числа из шестнадцатеричной системы счисления в десятичную необходимо его представить в виде многочлена, каждый элемент которого представлен в виде произведения цифры числа и соответствующей степени числа основания, в данном случае $16$, а затем нужно вычислить многочлен по правилам десятичной арифметики:
$X_{16} = A_n \cdot 16^{n-1} + A_{n-1} \cdot 16^{n-2} + A_{n-2} \cdot 16^{n-3} + ... + A_2 \cdot 16^1 + A_1 \cdot 16^0$
При переводе рекомендуется использовать таблицу 3.

Рисунок 3. Таблица 3
Число $FFA2_{16}$ перевести в десятичную систему счисления.
Решение. Используя приведенную таблицу $3$ степеней основания $8$, представим число в виде многочлена:
$FFA2_{16} = 15 \cdot 16^3 + 15 \cdot 16^2 + 10 \cdot 16^1 + 2 \cdot 16^0 =61440 + 3840 + 160 + 2 = 65442_{10}$
Правила перевода чисел из десятичной системы счисления в другую
- Для перевода числа из десятичной системы счисления в двоичную его необходимо последовательно делить на $2$ до тех пор, пока не останется остаток, меньший или равный $1$. Число в двоичной системе представить как последовательность последнего результата деления и остатков от деления в обратном порядке.
Число $22_{10}$ перевести в двоичную систему счисления.
Решение:
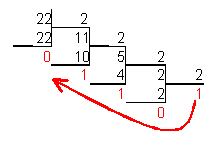
Рисунок 4.
$22_{10} = 10110_2$
- Для перевода числа из десятичной системы счисления в восьмеричную его необходимо последовательно делить на $8$ до тех пор, пока не останется остаток, меньший или равный $7$. Число в восьмеричной системе счисления представить как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Число $571_{10}$ перевести в восьмеричную систему счисления.
Решение:
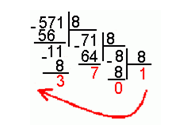
Рисунок 5.
$571_{10} = 1073_8$
- Для перевода числа из десятичной системы счисления в шестнадцатеричную систему его необходимо последовательно делить на $16$ до тех пор, пока не останется остаток, меньший или равный $15$. Число в шестнадцатеричной системе представить как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Число $7467_{10}$ перевести в шестнадцатеричную систему счисления.
Решение:
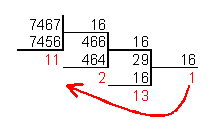
Рисунок 6.
$7467_{10} = 1D2B_{16}$
-
Для того чтобы перевести правильную дробь из десятичной системы счисления в недесятичную, необходимо дробную часть преобразуемого числа последовательно умножить на основание той системы, в которую ее требуется перевести. Дробь в новой системе будет представлена в виде целых частей произведений, начиная с первого.
Например: $0,3125_{(10)}$ в восьмеричной системе счисления будет выглядеть как $0,24_{(8)}$.
В данном случае можно столкнуться с проблемой, когда конечной десятичной дроби может соответствовать бесконечная (периодическая) дробь в недесятичной системе счисления. В данном случае количество знаков в дроби, представленной в новой системе, будет зависеть от требуемой точности. Также нужно отметить, что целые числа остаются целыми, а правильные дроби — дробями в любой системе счисления.
Правила перевода чисел из двоичной системы счисления в другую
- Чтобы перевести число из двоичной системы счисления в восьмеричную, его необходимо разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, затем каждую триаду заменить соответствующей восьмеричной цифрой согласно таблице 4.
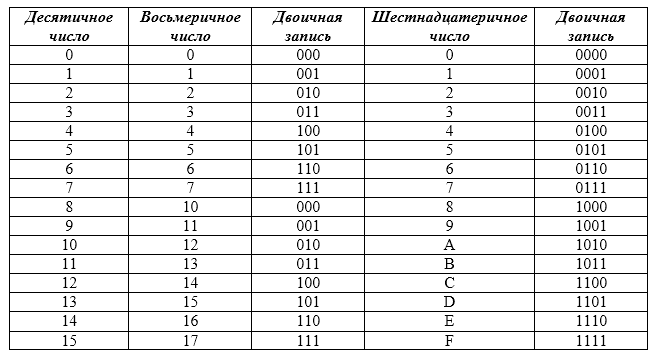
Рисунок 7. Таблица 4
Число $1001011_2$ перевести в восьмеричную систему счисления.
Решение. Используя таблицу 4, переведем число из двоичной системы счисления в восьмеричную:
$001 001 011_2 = 113_8$
- Чтобы перевести число из двоичной системы счисления в шестнадцатеричную, его следует разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, затем каждую тетраду заменить соответствующей восьмеричной цифрой согласно таблице 4.
Число $1011100011_2$ перевести в шестнадцатеричную систему счисления.
Решение. Используя таблицу 4 переведем число из двоичной системы счисления в шестнадцатеричную:
$0010 1110 0011_2 = 2E3_{16}$
Правила перевода чисел из любой системы счисления в двоичную
- Для перевода числа из восьмеричной системы счисления в двоичную следует каждую цифру заменить эквивалентной ей двоичной триадой, представленной в таблице 4.
Число $531_8$ перевести в двоичную систему счисления. Решение: $531_8 = 101011001_2$
- Для перевода числа из шестнадцатеричной системы счисления в двоичную требуется каждую цифру заменить эквивалентной ей двоичной тетрадой, представленной в таблице 4.
Число $EE8_{16}$ перевести в двоичную систему счисления.
Решение:
$EE8_{16} = 111011101000_2$
- При переводе числа из восьмеричной системы счисления в шестнадцатеричную и обратно, необходимо выполнить промежуточный перевод чисел в двоичную систему.
Число $FEA_{16}$ перевести в восьмеричную систему счисления.
Решение:
$FEA_{16} = 111111101010_2$
$111 111 101 010_2 = 7752_8$
Число $6635_8$ перевести в шестнадцатеричную систему счисления.
Решение:
$6635_8 = 110110011101_2$
$1101 1001 11012 = D9D_{16}$












